TAMAÑO DEL PROYECTO
El tamaño del proyecto es la capacidad que deberá instalarse para atender satisfactoriamente a la demanda del mercado objetivo y se expresa en volumen de producción o número de unidades que puede alojar, recibir, almacenar o producir una instalación en un periodo de tiempo específico. El tamaño determina los requerimientos de capital y, por consiguiente, una gran parte del costo fijo y es óptimo cuando opera con costo mínimo o máxima rentabilidad económica.
TAMAÑO DEL PROYECTO
El tamaño del proyecto es la capacidad que deberá instalarse para atender satisfactoriamente a la demanda del mercado objetivo y se expresa en volumen de producción o número de unidades que puede alojar, recibir, almacenar o producir una instalación en un periodo de tiempo específico. El tamaño es óptimo cuando opera con costo mínimo o máxima rentabilidad económica.
La capacidad se puede considerar de dos formas:
-
Como el índice máximo de producción por unidad de tiempo. Por ejemplo, la capacidad de una planta automotriz se podría medir como el número de automóviles que puede producir por semana.
-
Como unidades de la disponibilidad de un recurso. Por ejemplo, en el caso de un hospital la capacidad podría ser el número de camas disponibles para atender a los pacientes.
La capacidad de diseño
La capacidad de diseño es la producción teórica máxima por unidad de tiempo que puede lograr el proceso o sistema en un periodo dado y bajo condiciones de operación ideales. Para muchas empresas, medir la capacidad resulta sencillo: es el número máximo de unidades producidas en un tiempo específico. Sin embargo, para otras empresas, determinar la capacidad puede ser más difícil. La capacidad se puede medir en términos de camas (en un hospital), miembros activos (una iglesia) o tamaño de los salones de clase (una escuela). Otras organizaciones usan el tiempo de trabajo total disponible como medida de su capacidad global.
La mayoría de las organizaciones operan sus instalaciones a una tasa menor que la capacidad de diseño. Lo hacen porque han encontrado que pueden operar con más eficiencia cuando no tienen que extender sus recursos hasta el límite. En vez de esto, prefieren operar quizá a un 80% de la capacidad de diseño, este concepto se denomina capacidad efectiva.
La capacidad efectiva
La capacidad efectiva es la capacidad que una empresa espera alcanzar dadas las restricciones operativas actuales. La capacidad efectiva es menor que la capacidad diseñada cuando se toman en cuenta las pérdidas debidas al desperdicio, la fatiga de los trabajadores, las descomposturas del equipo y el mantenimiento. La capacidad efectiva se puede incrementar con mejoras operativas como procesos simplificados o un equipo que tiene requerimientos de mantenimiento más bajos.
Medidas de desempeño
Dos medidas de desempeño del sistema son particularmente útiles: la utilización y la eficiencia. La utilización es simplemente el porcentaje de la capacidad de diseño que realmente se logra. La eficiencia es el porcentaje de la capacidad efectiva que se alcanza en realidad, dependiendo de la forma en que se usen y administren las instalaciones, puede ser difícil o imposible de alcanzar el 100% de eficiencia. La clave para mejorar la eficiencia se encuentra frecuentemente en la corrección de los problemas de calidad, así como en una programación, capacitación y mantenimiento efectivos.
Para calcular la utilización y la eficiencia se usan las siguientes relaciones:
Ejemplo 1
Para un proyecto de inversión, se cuenta con la siguiente información:
-
Se ha decidido instalar una línea de producción que opere 7 días a la semana, en tres turnos de 8 horas al día y a una tasa de producción de 1,200 unidades por hora.
-
Durante el primer año se estima producir utilizando un 80% de la capacidad instalada.
Calcular:
-
La capacidad de diseño
-
La capacidad efectiva
Solución:
-
Capacidad de diseño = (7 días x 3 turnos x 8 horas) x (1,200 unidades por hora) = 201,600 unidades por semana.
-
Capacidad efectiva = 80% Capacidad de diseño = 0.8 (201,600) = 161,280 unidades por semana.
Ejemplo 2
Suponga que, durante la primera semana operativa del proyecto, la producción fue de 150,000 unidades. Calcular la utilización y la eficiencia de la capacidad.
-
Utilización = Producción real / capacidad de diseño = 150,000/201,600 = 0.744 = 74.4%
-
Eficiencia = Producción real / Capacidad efectiva = 150,000/161,280 = 0.93 = 93%
Ejemplo 3
Considere ahora que la empresa del ejemplo anterior, para satisfacer la demanda cada vez más creciente de su producto, necesita incrementar la producción agregando una segunda línea de producción.
La capacidad efectiva en la segunda línea es la misma que en la primera línea, es decir, 161,280 unidades. Como se calculó en el ejemplo 2, la primera línea opera con una eficiencia de 93%. Pero la producción en la segunda línea será menor debido a que el personal será primordialmente de nueva contratación; así que se espera que la eficiencia no sea mayor al 75%. ¿Cuál es la producción esperada entonces en esta segunda línea de producción?
Solución:
Producción esperada = Producción real, entonces:
Producción esperada = (Capacidad efectiva) (Eficiencia)
Producción esperada = (Capacidad efectiva) (Eficiencia) = (161,280) (0.75) = 120,960 unidades
Si la producción esperada es inadecuada podría necesitarse capacidad adicional.
CAPACIDAD EN FUNCIÓN DE LA DEMANDA
El estudio de mercado proporciona información para definir el nivel máximo del tamaño del proyecto. En efecto, un pronóstico preciso de la demanda resulta esencial para tomar una decisión sobre la capacidad. Cualquiera que sea el producto, se deben determinar los volúmenes de venta esperados y el ciclo de vida de los productos. Las decisiones sobre el tamaño del proyecto, en función de la demanda, son las siguientes:
-
Capacidad de planta mayor que el pronóstico de la demanda, con la expectativa de crecimiento en el futuro; sin embargo, se tendrá que evaluar el impacto de operar en los primeros periodos con costos mayores debido a la capacidad ociosa existente.
-
Capacidad de planta igual o inferior al pronóstico de la demanda, evaluando el riesgo de dejar demanda insatisfecha, permitir el ingreso de nuevos competidores, necesidad de incrementar la capacidad (turno extra, subcontratación, adquisición de nueva maquinaria y equipos, contratación de personal, etc.)
El pronóstico de la demanda y la distribución geográfica del mercado influyen en la decisión de definir una o varias plantas, de tamaño igual o diferente, en distintos lugares y con número de turnos también diferentes, sin embargo, se deberán considerar las economías de escala. Por ejemplo, las economías de escala harán recomendable una planta de mayor tamaño que cubra una mayor extensión geográfica; pero, esto hará subir los costos de distribución produciéndose una deseconomía de escala.
CASO 1: Planeación de la Capacidad en función de la Demanda
Un emprendedor quiere establecer la capacidad que requerirá en los próximos cinco años para sus dos líneas de producción de ciertos componentes de bronce y de plástico. Los componentes de bronce y los de plástico vienen en tres modelos A, B y C. El pronóstico de la demanda es el siguiente:

Las dos líneas de producción pueden fabricar todos los modelos. A continuación se especifica ciertas características de cada máquina:
Máquina de bronce
Capacidad de producción: 12,000 unidades por año
Operadores requeridos: 2 operadores por cada máquina
Moldeadora de Inyección
Capacidad de producción: 200,000 unidades por año
Operadores requeridos: 4 operadores por cada moldeadora
¿Qué capacidad se requerirá para los próximos cinco años?
Solución

Considerando la capacidad de producción de cada máquina y la cantidad de operadores necesarios, determinamos para cada línea de producción los requerimientos de capacidad (número de máquinas y operadores) para atender la demanda total. Por ejemplo, para la línea de componentes de plástico, los requerimientos de capacidad para el primer año se determinan de la manera siguiente: La cantidad de moldeadoras de inyección requerida para el primer año, se determina dividiendo la demanda total de componentes de plástico entre la capacidad de producción de una moldeadora de inyección, esto es:
Como se requieren 4 operadores por cada moldeadora, se necesitan un total de 0.6 moldeadoras por 4 operadores, que da un total de 2.4 operadores.
En forma similar se determinan los requerimientos de capacidad para la línea de componentes de bronce y luego se proyectan para todo el periodo de planeamiento.

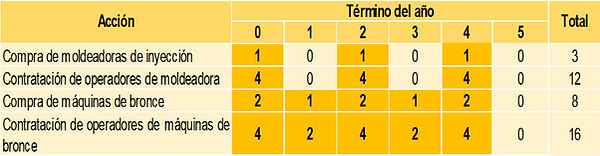
En la tabla se observa que, según la demanda máxima, los requerimientos de capacidad son los siguientes:
Número de Moldeadoras de Inyección : 3
Número de Operadores de Moldeadora : 12
Número de Máquinas de Bronce : 8
Número de Operadores de Máquina Bronce : 16
Sin embargo, por razones de disponibilidad de capital, financiamiento, obsolescencia física y tecnológica y otras que pudieran considerarse, las inversiones en la compra de maquinaria, así como en la contratación de los operadores de máquina, deben programarse adecuadamente para no afectar la atención de la demanda, tal como se muestra en la siguiente tabla:
CAPACIDAD EN TALLERES POR PROCESOS
En un taller por proceso, por lo común, el flujo de trabajo es fijo, el tiempo de preparación y de cambio es mínimo debido a que los bienes y servicios son estandarizados.
CASO 2: Medición de la Capacidad en Talleres por Procesos
Un proyecto de inversión considera un establecimiento para la producción de pizzas con dos empleados: Un chef de pizzas y un asistente; además estima la adquisición de un horno que tiene la capacidad de hornear 4 pizzas en 24 minutos. El proceso de transformación (secuencia de pasos) que se sigue en el establecimiento es el siguiente:

¿Cuál es la capacidad de este proceso?
Considerando que cada orden es de una pizza y que pueden añadirse pizzas al horno en cualquier momento durante el ciclo de cocinado, las capacidades de los recursos son.
El Asistente requiere 3 minutos por orden y puede procesar 20 órdenes por hora. En forma similar, se determina la capacidad de los otros recursos.
Asistente : 20 órdenes por hora
Chef : 12 órdenes por hora
Horno : 10 órdenes por hora
¿Cuál es el cuello de botella de este proceso?
Cuello de botella = 10 órdenes por hora (Horno)
El cuello de botella es el Horno, por tanto, el proceso no puede producir más de lo que puede procesar el cuello de botella, es decir, la capacidad del proceso es de 10 órdenes por hora.
Determinar la cantidad de recursos necesarios para atender la demanda, considerando la siguiente información:
Demanda promedio diaria : 164 órdenes por día
Jornada de trabajo : 8 horas por día

Si se necesitan 0.048780488 horas para atender una orden, entonces el ritmo de producción debe ser:

La cantidad mínima de recursos necesarios es la siguiente:
Producción del proceso balanceado:



Sin embargo, la cantidad requerida de recursos debe ser redondeada al entero superior:
Cantidad Asistentes = 2
Cantidad Chefs = 2
Cantidad Hornos = 3
Con esta cantidad de recursos, la capacidad de producción es la siguiente:
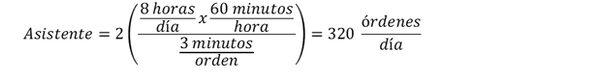
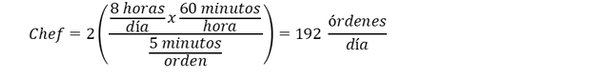

Capacidad del proceso = Min(320;192;240) = 192 órdenes por día
La capacidad de 192 órdenes por día permite atender cómodamente la demanda promedio de 164 órdenes por día y se tiene un colchón de capacidad igual a 28 órdenes por día.
CASO 3: CAPACIDAD EN TALLERES POR TRABAJO
En un taller por trabajo, el tiempo de preparación puede ser una parte significativa de la capacidad del sistema total y, por consiguiente, se debe incluir para determinar la capacidad.
La ecuación siguiente proporciona una expresión general para evaluar la capacidad requerida para cumplir con un volumen de producción determinado para una orden de trabajo i.

Donde:
C = Capacidad requerida
Ci = Requerimientos de capacidad en unidades de tiempo, por ejemplo: minutos, horas, días.
Si = Tiempo de preparación o de cambio para la orden de trabajo i, como una cantidad fija que no varía con el volumen.
Pi = Tiempo de procesamiento para cada unidad de la orden de trabajo, por ejemplo, horas/parte, minutos/operación, etc.
Qi = Volumen de la orden i en número de unidades
CASO 3: Medición de la Capacidad en Talleres por Trabajo
Manuel es un dentista profesional que trabaja un día de nueve horas, con una hora para comer y algunos momentos de descanso. Durante los primeros seis meses en que ha estado abierto su consultorio, él hace todo el trabajo, incluyendo limpieza y preparación para el siguiente procedimiento dental. María, su asistente administrativa, contesta el teléfono, se encarga de las facturas y también de las citas y los pagos. En la tabla 5.7 se muestran los tiempos de preparación y procesamiento para tres procedimientos. También se muestra el número de citas y la demanda de cada tipo.
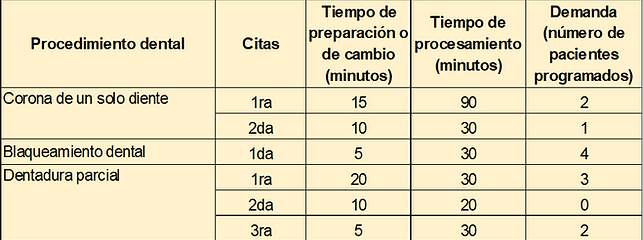
En un día particular Manuel ha programado dos primeras citas para coronas de un solo diente, una segunda cita para una corona de un solo diente, cuatro citas para blanquemiento dental, tres primeras citas y dos terceras citas para dentadura parcial ¿Manuel tiene la capacidad para desempeñar todo este trabajo?
Solución:
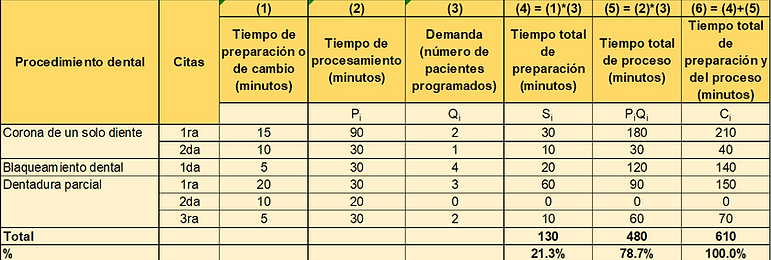
Realizando los cálculos necesarios que se muestran en la tabla anterior se determina que Manuel está programando un total de 610 minutos de trabajo durante una jornada de 480 minutos. Por consiguiente, hay una escasez de capacidad de 130 minutos. Manuel tendrá que trabajar 2 horas y 10 minutos más, o bien reprogramar a algunos clientes.
En este caso particular, se supone una preparación para cada cliente, por esta razón, por ejemplo, el tiempo total de preparación para atender a los dos clientes en primera cita de corona de un solo diente es igual a 15*2=30 minutos, es decir 15 minutos para cada paciente.
Según el análisis, 21.3% de la capacidad total se utiliza para preparaciones y cambios de un proceso dental al siguiente. Si contrata a un asistente o un técnico dental para que desempeñe ese trabajo (suponiendo que eso se pueda hacer a un lado mientras Manuel sigue trabajando con otros pacientes), Manuel tendría una capacidad libre de 21.3% para atender otros pacientes e incrementar sus ingresos. Si pudiera reducir 50% su tiempo de preparación, únicamente requeriría 65 minutos extras de su tiempo.
Los tiempos de preparación por lo común representan un porcentaje considerable de la capacidad total de la mayoría de los talleres por trabajo. Es necesario esforzarse para reducir el tiempo de preparación a la cantidad más baja posible, con el fin de liberar la capacidad para crear producción.
CASO 4: CAPACIDAD EN SISTEMAS DE PRODUCCIÓN POR PRODUCTO (PROCESO CONTINUO)
El cálculo del tamaño o capacidad de un sistema de producción por producto, en proceso continuo, se realiza a través del siguiente procedimiento:
-
Elaborar el diagrama de bloque del proceso de producción del producto estandarizado.
-
Determinar el balance de materia en el cual se especifican las cantidades entrantes y salientes en cada operación; se forma una secuencia en la cual las cantidades salientes de una operación resultan las cantidades de entrada de la siguiente.
-
Calcular la capacidad de cada operación en función de las unidades de entrada o de salida, según conveniencia (en todo caso será muy sencillo migrar de una a otra unidad usando el balance de material).
-
Homogeneizar las capacidades parciales mediante un factor de conversión que las exprese en unidades homogéneas de producto terminado, considerando para ello los cambios físicos o químicos sufridos por el material en cada operación.
-
Establecer la capacidad de todo el sistema, determinando la operación cuello de botella, la cual corresponde a aquella operación que tiene el mayor tiempo de ejecución, o lo que es equivalente: la menor productividad.
En un proceso continuo, la transformación de la materia prima o del insumo principal, va recibiendo valor agregado y finalmente se convierte en un producto terminado. La capacidad podrá ser expresada en capacidad de procesamiento (entrada) o en capacidad de producción (salida).
Caso
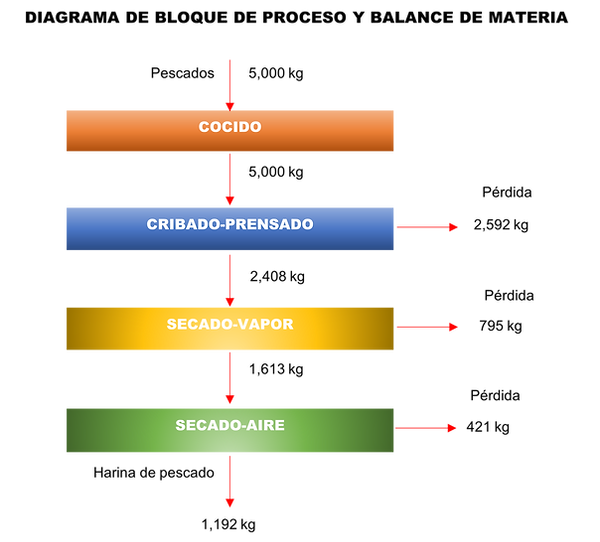
En un proyecto para producir harina de pescado, el estudio técnico recomienda considerar la siguiente información para determinar el tamaño del proyecto:
Demanda por semana: K = 500 kg
Para todas las operaciones:
Días por semana: D = 7
Horas reales por turno: H = 8
Turnos por día: T = 3
Factor de Utilización: U = 0.9
Eficiencia: E = 0.95
El factor de utilización, es el cociente entre el número de horas productivas desarrolladas y el de horas reales de jornada por periodo. En este caso, de la jornada de 8 horas de un día, se pierde, por diversos motivos, 48 minutos, equivalente a 0.8 horas por día, entonces el factor de utilización es igual a 0.9.
El factor de eficiencia es el cociente entre el número de horas estándar y el número de horas productivas desarrolladas. Para nuestro caso, sin considerar el balance de material, la operación cuello de botella es Secado-Aire que produce 2.2 kg por hora, es decir emplea 0.454545454545455 horas para procesar un kg. Ahora, considerando que esta operación que requiere 0.454545454545455 horas estándar, se desarrollará 105 veces a la semana, empleando 50.4 (7*7.2) horas productivas, la eficiencia resultante es 0.95.
Otros datos técnicos:
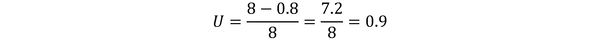

Capacidad de procesamiento:
La capacidad de producción expresada en capacidad de procesamiento (entrada), puede calcularse con la siguiente fórmula:
Donde:
C1 = Capacidad de procesamiento
P = Producción por hora de cada máquina
M = Número de máquinas
D = Días de trabajo por semana
H = Horas reales por turno
T = Turnos por día
U = Factor de utilización
E = Eficiencia
Factor de conversión:
Es la relación entre el producto terminado (F) y cada cantidad entrante en cada operación (Q).
Capacidad de producción:
La capacidad expresada en capacidad de producción (salida) puede calcularse con la siguiente fórmula:
A continuación se presenta un esquema simplificado del proceso de producción:

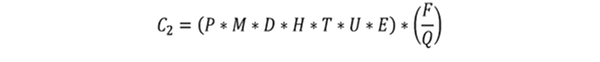
De la fórmula de la capacidad de producción, despejamos M (número de máquinas):
Haciendo C2 = Demanda. se obtiene:
Ahora, calculamos el número de máquinas requeridas en cada operación para poder atender la demanda semanal de 500 kg de producto terminado.
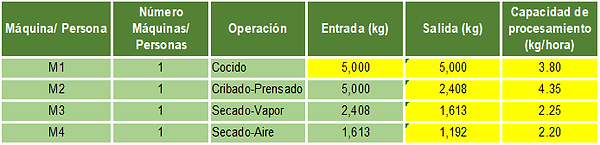
Operación Cocido:
Con esta cantidad fraccionaria de máquinas, se verifica que se cumple con una producción para atender la demanda semanal de 500 kg de harina de pescado:
Como se está planeando trabajar en tres turnos, no existe la posibilidad de comprar tres máquinas y trabajar turnos extras para cumplir con la demanda, por esta razón necesariamente se tiene que comprar 4 máquinas, con lo cual la capacidad semanal de la operación de cocido es:
Operación Cribado-Prensado:
Si M = 4, entonces la capacidad semanal de esta operación es:
Operación Secado-Vapor:
Si M = 4, entonces la capacidad semanal de esta operación es:
Mediante un procedimiento similar se calcula el número de máquinas y la capacidad semanal de las demás operaciones, cuyos resultados se presenta en la siguiente tabla:


Con estos resultados, la capacidad del sistema de producción es igual a la capacidad del "cuello de botella", esto es:
Capacidad sistema producción = mín (520.5053952;595.8417024;639.9376744;700.5856218) = 520.5053952 kg de harina de pescado por semana.
CASO 5: TAMAÑO Y LOCALIZACIÓN DEL PROYECTO
En un proyecto emprendedor de gran escala, para introducir un nuevo producto, se debe decidir sobre el sitio y el tamaño de las plantas industriales. El objetivo es minimizar los costos de producción y distribución, así como los de construcción y operación de las instalaciones.
Hay tres sitios disponibles A, B y C. Puede construirse una planta pequeña o una mediana o una grande en cada sitio. La Tabla N°1 muestra los costos y capacidades para estas opciones; en el costo anual se incluyen los gastos generales de fabricación y un costo anual para la construcción.
El proyecto debe suministrar el producto a cuatro regiones. El costo de distribución desde cada planta hasta cada región; y los requerimientos de las regiones se encuentran en la Tabla N°2.
El problema es decidir sobre los sitios a utilizar, cuál debe ser el tamaño de la planta en los sitios seleccionados y cuánto debe enviar cada planta a cada región.


Solución:
Este problema se modela matemáticamente con programación lineal y se resuelve aplicando el complemento Solver de Excel.
Se recomienda visitar la página sobre LOCALIZACIÓN donde se desarrollan varios casos de este tipo.
Variables del modelo:
A1 = envíos desde el sitio A hacia la Región-1 (en unidades)
A2 = envíos desde el sitio A hacia la Región-2 (en unidades)
A3 = envíos desde el sitio A hacia la Región-3 (en unidades)
A4 = envíos desde el sitio A hacia la Región-4 (en unidades)
B1 = envíos desde el sitio B hacia la Región-1 (en unidades)
B2 = envíos desde el sitio B hacia la Región-2 (en unidades)
B3 = envíos desde el sitio B hacia la Región-3 (en unidades)
B4 = envíos desde el sitio B hacia la Región-4 (en unidades)
C1 = envíos desde el sitio C hacia la Región-1 (en unidades)
C2 = envíos desde el sitio C hacia la Región-2 (en unidades)
C3 = envíos desde el sitio C hacia la Región-3 (en unidades)
C4 = envíos desde el sitio C hacia la Región-4 (en unidades)
PPA = producción de la planta pequeña localizada en el sitio A (en unidades)
PMA = producción de la planta mediana localizada en el sitio A (en unidades)
PGA = producción de la planta grande localizada en el sitio A (en unidades)
PPB = producción de la planta pequeña localizada en el sitio B (en unidades)
PMB = producción de la planta mediana localizada en el sitio B (en unidades)
PGB = producción de la planta grande localizada en el sitio B (en unidades)
PPC = producción de la planta pequeña localizada en el sitio C (en unidades)
PMC = producción de la planta mediana localizada en el sitio C (en unidades)
PGC = producción de la planta grande localizada en el sitio C (en unidades)
YPA = variable cero/uno con entero, que es 1 si se construye una planta pequeña en el sitio A, 0 si es de otro modo
YMA = variable cero/uno con entero, que es 1 si se construye una planta mediana en el sitio A, 0 si es de otro modo
YGA = variable cero/uno con entero, que es 1 si se construye una planta grande en el sitio A, 0 si es de otro modo
YPB = variable cero/uno con entero, que es 1 si se construye una planta pequeña en el sitio B, 0 si es de otro modo
YMB = variable cero/uno con entero, que es 1 si se construye una planta mediana en el sitio B, 0 si es de otro modo
YGB = variable cero/uno con entero, que es 1 si se construye una planta grande en el sitio B, 0 si es de otro modo
YPC = variable cero/uno con entero, que es 1 si se construye una planta pequeña en el sitio C, 0 si es de otro modo
YMC = variable cero/uno con entero, que es 1 si se construye una planta mediana en el sitio C, 0 si es de otro modo
YGC = variable cero/uno con entero, que es 1 si se construye una planta grande en el sitio C, 0 si es de otro modo
Formulación del modelo:
Minimizar:
A1 + 2A2 + 3A3 + 4A4 + 2B1 + 3B2 + 2B3 + 3B4 + 4C1 + 3C2 + 2C3 + C4 + 5PPA + 4PMA + 3PGA + 5PPB + 4PMB + 3.5PGB + 6PPC + 5PMC + 4PGC + 1,000,000YPA + 1,300,500YMA + 1,500,650YGA + 1,200,860YPB + 1,600,400YMB + 2,100,500YGB + 900,850YPC + 1,250,580YMC + 1,450,500YGC
Sujeta a:
Requerimientos Región-1: A1 + B1 + C1 ≥ 500,800
Requerimientos Región-2: A2 + B2 + C2 ≥ 200,600
Requerimientos Región-3: A3 + B3 + C3 ≥ 700,900
Requerimientos Región-4: A4 + B4 + C4 ≥ 980,700
Producción en A: A1 + A2 + A3 + A4 - PPA - PMA - PGA ≤ 0
Producción en B: B1 + B2 + B3 + B4 - PPB - PMB - PGB ≤ 0
Producción en C: C1 + C2 + C3 + A4 - PPC - PMC - PGC ≤ 0
Capacidad en A pequeña: PPA - 600,000YPA ≤ 0
Capacidad en A mediana: PMA - 850,000YMA ≤ 0
Capacidad en A grande: PGA - 1,250,000YGA ≤ 0
Capacidad en B pequeña: PPB - 600,000YPB ≤ 0
Capacidad en B mediana: PMB - 1,200,000YMB ≤ 0
Capacidad en B grande: PGB - 2,000,000YGA ≤ 0
Capacidad en C pequeña: PPC - 600,000YPC ≤ 0
Capacidad en C mediana: PMC - 900,000YMC ≤ 0
Capacidad en C grande: PGC - 2,000,000YGC ≤ 0
Máximo una planta en A: YPA + YMA + YGA ≤ 1
Máximo una planta en B: YPB + YMB + YGB ≤ 1
Máximo una planta en C: YPC + YMC + YGC ≤ 1
Todas las variables ≥ 0
YPA, YMA, YGA, YPB, YMB, YGB, YPC, YMC, YGC son variables binarias con enteros
SOLUCIÓN CON SOLVER DE EXCEL

Solución:
Ubicación de Plantas
Instalar en el sitio A una planta grande con capacidad de 1,250,000 unidades.
Instalar en el sitio C una planta grande con capacidad de 1,200,000 unidades.
Envíos de cada planta a cada región
De la planta grande instalada en el sitio A, con capacidad de 1,250,000 unidades, se envía 500,800 unidades a la Región-1; 200,600 unidades a la Región-2; y 548,600 unidades a la Región-3.
De la planta grande instalada en el sitio C, con capacidad de 1,200,000 unidades, se envía 152,300 unidades a la región-3, y 980,700 unidades a la Región-4.
Exceso de capacidad
En la planta grande localizada en el sitio C, existe un exceso de capacidad igual a 67,000 unidades.
Costo Total
El costo total es igual a S/15,066,250 de los cuales S/2,951,150 son fijos y S/12,115,100 variables.
TAMAÑO DEL PROYECTO
El tamaño del proyecto es la capacidad que deberá instalarse para atender satisfactoriamente a la demanda del mercado objetivo y se expresa en volumen de producción o número de unidades que puede alojar, recibir, almacenar o producir una instalación en un periodo de tiempo específico. El tamaño es óptimo cuando opera con costo mínimo o máxima rentabilidad económica.
La magnitud del tamaño o capacidad productiva del proyecto incidirá significativamente sobre el nivel de las inversiones y de los costos y, en consecuencia, sobre la rentabilidad del proyecto. Por esta razón, las decisiones sobre el tamaño deben estar integradas en la misión y la estrategia de la empresa, es decir, las inversiones en capacidad no deben realizarse como gastos aislados, sino como parte de un plan coordinado para lograr ventaja competitiva y obtener utilidades sostenidas. Las preguntas que deben hacerse son: ¿Estas inversiones nos permitirán ganar clientes en algún momento? y ¿Qué ventajas competitivas (como flexibilidad del proceso, velocidad de entrega, mejoramiento de la calidad, etc.) obtendremos?



