LOCALIZACIÓN DE PLANTAS Y CENTROS DE DISTRIBUCIÓN
La localización de plantas y centros de distribución es una decisión estratégica y de naturaleza diversa ya que la distribución de los productos, forman una cadena de suministro que comprende tanto la distribución de insumos entre diferentes plantas, como la de productos terminados hacia los centros de distribución y tiendas.

MODELO DE PLANTA CON CAPACIDAD LIMITADA
Permite definir la configuración regional de las instalaciones.
El objetivo es decidir cuál es el diseño de la red que maximiza las utilidades después de impuestos. Sin embargo, para efectos de simplicidad, suponemos que toda la demanda debe satisfacerse y se pasan por alto los impuestos sobre las utilidades. De esta manera, el modelo se enfoca en minimizar el costo de satisfacer la demanda global.
Datos:
n = número de posibles localizaciones y capacidades de la planta (cada nivel de capacidad contará como una ubicación separada)
m = número de mercados o puntos de demanda
Di = demanda anual del mercado j
ki = capacidad de la planta i
fi = costo fijo anualizado de mantener la fábrica i abierta
cij = costo de producir y enviar una unidad desde la fábrica i al mercado j (el costo incluye producción, inventario, transporte y aranceles)
Variables de decisión:
Yi = 1 si la planta i está abierta, 0 si está cerrada
Xij = cantidad enviada desde las planta i al mercado j
Modelo de Programación Lineal:
Función Objetivo: Minimizar el costo total (fijo + variable) de construir y operar la red de la cadena de suministro.

Restricciones:
Restricciones de demanda: La demanda de cada mercado debe ser satisfecha.
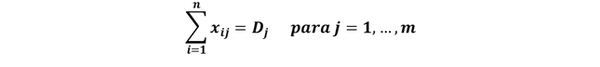
Restricciones de capacidad:
Ninguna planta puede producir más de los que permite su capacidad.

Restricciones de operación de las plantas:
La capacidad es "0" si la planta está cerrada y "k" si está abierta. El producto "ky" capta este efecto.
CASO 1
Un proyecto de una empresa para vender en todo el mundo puede considerar varias opciones para satisfacer la demanda.
-
Una posibilidad es construir una instalación en cada región, país o ciudad. La ventaja de este método es que disminuye los costos de transporte y ayuda a evitar los aranceles que pueden ser impuestos si el producto es importado de otras regiones. La desventaja de este método es que las dimensiones de las plantas se determinan para satisfacer la demanda local y pueden no explotar del todo las economías de escala.
-
Un método alternativo es consolidar las plantas en algunas regiones o países. Esto mejora las economías de escala, pero incrementa los costos de transporte y los impuestos.
El Proyecto debe considerar estos balances cuantificables junto con los factores no cuantificables, como el ambiente competitivo y el riesgo político.
Consideremos que se ha recolectado la información agregada que se muestra en la siguiente tabla:
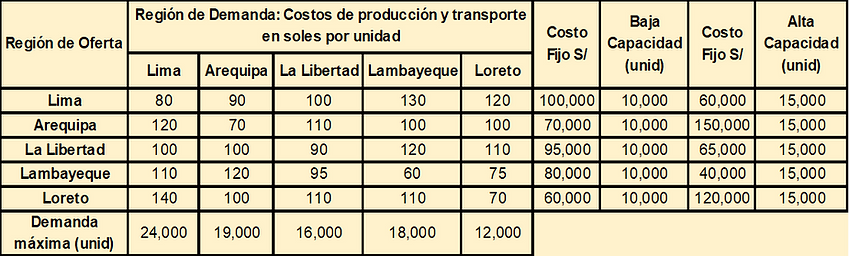
MODELO DE PROGRAMACIÓN LINEAL
Variables de decisión:
Xij = cantidad enviada desde i hasta j
Yi = 1 si la planta i está abierta; 0 si está cerrada
Función objetivo:
Min 60,000Y1 + 100,000Y2 + 150,000Y3 + 70,000Y4 + 65,000Y5 + 95,000Y6 + 40,000Y7 + 80,000Y8 + 120,000Y9 + 60,000Y10 + 80X11 + 90X12 +...+ 120X15 + 120X21 + …+ 100X25 + 100X31 + ...+ 110X35 + 110X41 + .. + 75X45 + 140X51 + … + 70X55
Restricciones de demanda:
X11 + X21 + X31 + X41 + X51 = 24,000, demanda Región Lima
X12 + X22 + X32 + X42 + X52 = 19,000, demanda Región Arequipa
X13 + X23 + X33 + X43 + X53 = 16,000, demanda Región La Libertad
X14 + X24 + X34 + X44 + X54 = 18,000, demanda Región Lambayeque
X15 + X25 + X35 + X45 + X55 = 12,000, demanda Región Loreto
Restricciones de capacidad:
X11 + X12 + X13 + X14 + X15 - 15,000Y1 - 10,000Y2 ≤ 0, capacidad Región Lima
X21 + X22 + X23 + X24 + X25 -15,000Y3 - 10,000Y4 ≤ 0, capacidad Región Arequipa
X31 + X32 + X33 + X34 + X35 - 15,000Y5 - 10,000Y6 ≤ 0, capacidad Región La Libertad
X41 + X42 + X43 + X44 + X45 - 15,000Y7 - 10,000Y8 ≤ 0, capacidad Región Lambayeque
X51 + X52 + X53 + X54 + X55 - 15,000Y9 - 10,000Y10 ≤ 0, capacidad región Región Loreto
Restricciones de no negatividad:
Xij ≥0, para i=1,…,5; j=1,…,5
Restricciones de números binarios:
Yi ϵ {0,1}, para i=1,…,10
SOLUCIÓN CON SOLVER DE EXCEL
Costo Total: S/7,250,000 (Costo Fijo: S/625,000; Costo Variable: S/6,625,000)

La solución óptima es la siguiente:
-
Dos plantas ubicadas en Lima, una con capacidad baja de 10,000 unidades y otra con capacidad alta de 15,000 para atender la demanda de Lima igual a 24,000 unidades. Existe un exceso de capacidad de 1,000 unidades.
-
Dos plantas ubicadas en Arequipa, una con capacidad baja de 10,000 unidades y otra con capacidad alta de 15,000 para atender la demanda de Arequipa (19,000 unidades). Existe un exceso de capacidad de 6,000 unidades.
-
Una planta ubicada en La Libertad con capacidad alta de 15,000 unidades, para atender la demanda de La Libertad (15,000 unidades).
-
Dos plantas ubicadas en Lambayeque, una con capacidad baja de 10,000 unidades y otra con capacidad alta de 15,000 para atender la demanda de La Libertad (1,000 unidades), la demanda de Lambayeque (18,000 unidades) y la demanda de Loreto (2,000 unidades). Existe un exceso de capacidad de 4,000 unidades.
-
Una planta ubicada en Loreto con capacidad baja de 10,000 unidades, para atender la demanda de Loreto (10,000 unidades).
Exceso de capacidad
En Lima queda un exceso de capacidad de 1,000 unidades.
En Arequipa queda un exceso de capacidad de 6,000 unidades.
En Lambayeque queda un exceso de capacidad de 4,000 unidades.
MODELO DEL CENTRO DE GRAVEDAD
Proceso sistemático de búsqueda a partir de un punto llamado centro de gravedad que es la localidad que minimiza la distancia ponderada entre la instalación que produce los bienes o provee el servicio y los clientes a los que se destina la nueva instalación.
A continuación, analizamos un modelo de gravedad para localizar una instalación que recibe materias primas de las fuentes de suministro y envía productos terminados a los mercados y se conocen los costos de envío. Los datos básicos de este modelo de gravedad son los siguientes:
xi, yi: coordenadas de la localización de un mercado o una fuente de suministro i.
Ci: costo de enviar una unidad por kilómetro entre la instalación y el mercado o la fuente de suministro i.
Qi: cantidad que se enviará entre la instalación y el mercado o la fuente de suministro i.
Si (x,y) es la localización seleccionada para la instalación, la distancia, di, entre la instalación en esa localización (x,y) y la fuente de suministro o mercado i está dada por:
y el costo total (CT) de transporte se determina mediante la siguiente relación:
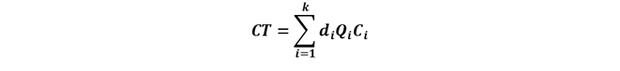
La ubicación óptima es la que minimiza el costo total y se obtiene empleando la herramienta Solver de Excel como se explica en el siguiente ejemplo. En este caso usaremos distancias euclidianas, pero también se puede usar las distancias rectilíneas.
CASO 2
Supongamos que una empresa está planeando la localización más adecuada para una nueva instalación y desea seleccionar un sitio en el cual se minimicen las distancias que deben recorrer las cargas, sobre todo las más grandes, desde y hacia él. Según la industria de que se trate, la carga puede consistir en embarques enviados por proveedores, transportados entre plantas o enviados a clientes, pero también puede consistir en clientes o empleados que viajan hacia o desde la instalación.
ALFA SAC, un fabricante de refrigeradoras, tiene una fábrica de ensamblaje desde la cual abastece a todos sus mercados. La demanda ha crecido con rapidez, por lo que la empresa ha decidido construir otra fábrica para la cual debe encontrar una ubicación adecuada.
Existen tres plantas localizadas en Callao, Trujillo y Arequipa que proveerán partes a la nueva fábrica, la cual atenderá los mercados en Lima, Chiclayo, Piura, Huancayo y Cuzco.
Las coordenadas de localización, la demanda de cada mercado, el suministro de partes requerido de cada planta y el costo de envío para cada fuente de abastecimiento o mercado se muestran en la siguiente tabla:

SOLUCIÓN ÓPTIMA CON SOLVER DE EXCEL
Se identifica las coordenadas X = 713 km e Y = 876 km, como la ubicación de la planta que minimiza el costo de transporte total igual a S/133,243,567.
Finalmente, en un mapa, se deberá ubicar las coordenadas encontradas para determinar la localización geográfica de la nueva planta de producción.
Al superponer un mapa que contenga las ubicaciones de las Fuentes y Mercados y todas las localidades aledañas, se encontrará la localización que corresponda a las coordenadas X = 713 km e Y = 876 km.

MODELO DE RANKING DE FACTORES
Los modelos de gravedad ayudan a ubicar la zona alrededor de la cual es conveniente localizar la planta o centro de distribución, de manera que los costos de transporte no sean altos. Sin embargo, la ubicación obtenida no reúne necesariamente todas las características que requiere el proyecto (condiciones laborales, disponibilidad de servicios, fuentes de energía, etc.). En consecuencia, es necesario identificar localidades candidatas que reúnan las características cualitativas para que la planta o el centro de distribución opere satisfactoriamente. La técnica más difundida para este propósito es la calificación de los factores ponderados de localización o matriz de preferencias de localización que consta de los siguientes pasos:
-
Desarrollar una lista de los factores relevantes sobre la localización y clasificarlos en las categorías de dominantes y secundarios.
-
Asignar un peso a cada factor que refleje su importancia relativa en cuanto a los objetivos del proyecto. Cada peso o ponderación refleja la percepción de la importancia de cada factor, y típicamente el total de esos pesos es 1 ó 100%.
-
Desarrollar una escala para cada factor (por ejemplo, de 1 a 10 o de 1 a 100 puntos).
-
Hacer que el equipo emprendedor califique cada factor para cada localización, usando la escala del paso 3.
-
Multiplicar la calificación por los pesos de cada factor y sumar los puntos de cada localización.
-
Hacer una recomendación basada en la calificación de mayor puntaje, considerando también los resultados de los enfoques cuantitativos.
CASO 3
Un proyecto de inversión, relacionado con la producción y comercialización de cocinas a gas, ha decidido localizarse en provincias mediante la apertura de una planta en la región norte de nuestro país. Desea seleccionar entre Trujillo o Chiclayo. La tabla siguiente muestra los factores de localización que se consideró importantes; asimismo, muestra las ponderaciones y las calificaciones para dos sitios posibles: Moshoqueque en Chiclayo y Parque Industrial de Trujillo.
Escala de calificación
Excelente 9 - 10 puntos
Muy Bueno 7 - 8 puntos
Bueno 5 - 6 puntos
Regular 3 - 4 puntos
Deficiente 1 - 2 puntos

Es preferible la localización en Moshoqueque (Chiclayo) porque esta localidad tiene la mayor suma ponderada igual a 7.67 puntos.
CASO 4
En este último ejemplo presentamos otra forma de aplicación de este método.
Paso 1: Definición de los factores de localización
Hacer un listado de los factores relevantes de localización según el sector industrial al que pertenece el proyecto.
Supongamos que para nuestro proyecto se definieron los siguientes factores de localización:
F1: Cercanía al mercado
F2: Vías de acceso
F3: Restricciones municipales
F4: Disponibilidad y costo de locales
F5: Disponibilidad y costo de energía
F6: Disponibilidad, calidad y costo de materiales
F7: Disponibilidad y costo de mano de obra calificada
Paso 2: Elaboración de la Matriz de Enfrentamiento
Analizar el nivel de importancia relativa de cada uno de los factores y asignarles una ponderación o peso relativo considerando los siguientes criterios:
-
Incidencia del factor sobre las operaciones de la futura empresa
-
Importancia estratégica de una buena selección
-
Proyección de su relevancia en el tiempo
Con estos criterios se evalúa la importancia relativa de cada factor con respecto a otro factor; para esta evaluación se utiliza una Matriz de Enfrentamiento como la siguiente que corresponde a nuestro ejemplo.

La evaluación se realiza aplicando las reglas siguientes:
-
Asignar el valor de uno (1) a aquel factor "más importante" que el factor con el cual se compara.
-
Asignar el valor de cero (0) si el factor analizado es "menos importante" que el factor con el cual es comparado.
-
En casos donde la "importancia es equivalente", ambos factores tendrán el valor uno (1) en el casillero correspondiente.
-
En la columna del extremo derecho de la Matriz de Enfrentamiento se contabilizan los puntos para cada factor y se determina el porcentaje correspondiente, el cual representa la ponderación de cada factor.
Paso 3: Propuesta de alternativas de localización
Se realiza un análisis de diferentes lugares ubicados en el área de influencia del proyecto que cumplan con un nivel mínimo de desarrollo de cada uno de los factores y se les propone como alternativas de localización.
Consideremos las siguientes alternativas de localización en el distrito de Los Olivos:
Local ubicado en Zona-1
Local ubicado en Zona-2
Local ubicado en Zona-3
Paso 4: Escala de calificación
Se debe estudiar cada factor y evaluar su nivel de importancia de desarrollo en cada alternativa de localización. Se requiere tener información completa de cada factor de localización con respecto a cada factor y luego asignar una calificación a cada factor en cada alternativa de localización mediante una escala de calificación como la siguiente:
Excelente 9 - 10 puntos
Muy Bueno 7 - 8 puntos
Bueno 5 - 6 puntos
Regular 3 - 4 puntos
Deficiente 1 - 2 puntos
Paso 5: Tabla de Ranking de Factores
La Tabla de Ranking de Factores se desarrolla de la siguiente manera:
-
Evaluar el puntaje que deberá tener cada factor en cada localidad.
-
Multiplicar la ponderación por la calificación.
-
Para cada alternativa de localización se realiza la sumatoria de los puntajes.
-
Finalmente, aquella localidad que tenga el mayor puntaje es elegida como el lugar adecuado para localizar el proyecto.
Para nuestro ejemplo, en la tabla siguiente se presenta la tabla de ranking de factores de localización.

Según los resultados obtenidos en la Tabla Ranking de Factores, se decide por la Zona-1 porque esta zona tiene la mayor suma ponderada igual a 8.76 puntos.
ANÁLISIS DEL PUNTO DE EQUILIBRIO
El análisis del punto de equilibrio de la localización es el uso del análisis de costo-volumen para hacer una comparación económica de las alternativas de localización. Al identificar los costos fijos y variables y graficarlos para cada localización, podemos determinar cuál proporciona el menor costo.
El análisis del punto de equilibrio de la localización se realiza en forma gráfica o matemática. El enfoque gráfico tiene la ventaja de dar un intervalo del volumen para el que es preferible cada localización. Los tres pasos para efectuar el análisis del punto de equilibrio de la localización son los siguientes:
-
Determinar los costos fijos y variables para cada localización.
-
Graficar los costos de cada localización, con los costos en el eje vertical y el volumen anual en el eje horizontal.
-
Seleccionar la localización que tenga el menor costo total para el volumen de producción esperado.
CASO 5
El equipo emprendedor está considerando tres localizaciones para ubicar la planta de producción: A, B y C. El objetivo es encontrar la localización más económica para un volumen de demanda esperada igual a 2,000 unidades por año.
Se decide por un análisis del punto de equilibrio de la localización. Para realizarlo se determinó el precio de venta esperado por unidad y la estructura de costos según se indica a continuación:
Precio Venta =S/120 por unidad
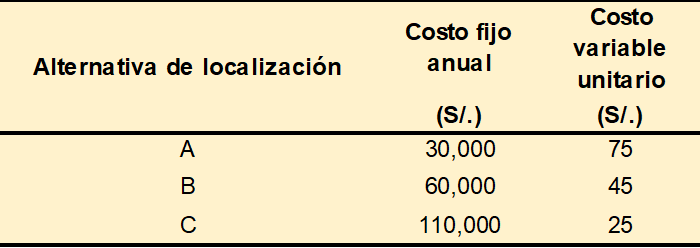
Paso 1: Funciones de costos totales para cada localización
Costo total = Costo fijo + Costo variable: C = F + vQ
Donde: C = Costo total; F = Costo fijo anual; v = Costo variable unitario y Q = volumen de producción

Paso 2: Gráfica de las funciones de costos
Como las funciones de costos son lineales, para graficarlas necesitamos conocer dos puntos para cada función. Un punto será el cruce de la función con el eje vertical y otro el cruce con otra función. La escala de los valores que se ingresen en las celdas de color amarillo deben incluir a los puntos de intercepción de las funciones de costos.

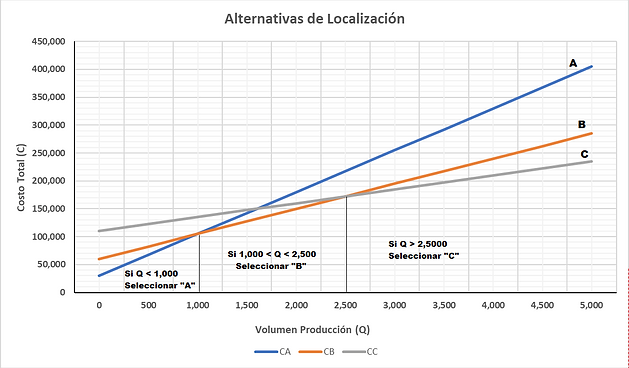
Cruce con el eje vertical: Se determina haciendo Q = 0 en cada función:
Cruce de "A" con el eje vertical: Punto intercepción (0,30000)
Cruce de "B" con el eje vertical: Punto intercepción (0,60000)
Cruce de "C" con el eje vertical: Punto intercepción (0,110000)
Cruce entre dos funciones de costos:
"A" y "B": CA = CB, de donde: Q =1,000; C = 105,000; Punto intercepción (1000,105000)
"A" y "C": CA = CC, de donde: Q =1,600; C = 150,000; Punto intercepción (1600,150000)
"B y "C": CB = CC, de donde: Q =2,500; C= 172,500; Punto intercepción (2500,172500)
Plan de Localización:

ANÁLISIS DE LA INVERSIÓN
En el análisis de las inversiones impulsadas por las decisiones de localización, se aplica el análisis de inversión tradicional con los criterios del Valor Presente Neto (VPN) o del Valor Anual Uniforme.
CASO 6: ALTERNATIVAS DE LOCALIZACIÓN MUTUAMENTE EXCLUYENTES CON VIDAS ÚTILES O DE SERVICIO IGUALES
Un proyecto de inversión está considerando la posibilidad de localizar una tienda comercial. Existen dos localidades candidatas para la localización para las cuales se dispone de la siguiente información.

¿Qué localidad debe elegirse considerando una Tasa Mínima Atractiva de Rendimiento (TMAR) de 14%?
SELECCIÓN DE ALTERNATIVAS DE LOCALIZACIÓN MUTUAMENTE EXCLUYENTES CON VIDA ÚTILES IGUALES POR EL MÉTODO DEL VALOR PRESENTE NETO (VPN)
Cuando los costos o flujos de efectivo anuales son uniformes, puede usarse la siguiente fórmula para hallar el VPN, caso contrario cada costo o flujo de efectivo anual tiene que ser traído al presente en forma individual.
Donde:
VPN = Valor presente neto
I = Costo inicial (inversión)
A = Costo de operación anual
i = Tasa de interés o tasa mínima atractiva de rendimiento(TMAR)
S = Valor de salvamento al término de la vida útil
n = Vida útil o de servicio




Según el criterio del VPN, la Localización A es más económica y, por lo tanto, sería preferible.
SELECCIÓN DE ALTERNATIVAS DE LOCALIZACIÓN MUTUAMENTE EXCLUYENTES CON VIDA ÚTILES IGUALES POR EL MÉTODO DEL VALOR ANUAL UNIFORME EQUIVALENTE (VAUE)
Como ya hemos calculado el VPN de cada alternativa, el VAUE puede determinarse mediante la siguiente fórmula:


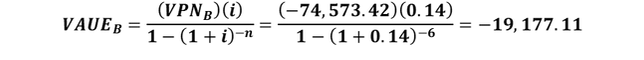
Según el criterio del VAUE, también se verifica que la localización A es más económica y es la que debe elegirse.
Si no se hubiera calculado previamente el VPN, el VAUE se tendría que calcular con la siguiente fórmula:


CASO 7: ALTERNATIVAS DE LOCALIZACIÓN MUTUAMENTE EXCLUYENTES CON VIDAS ÚTILES O DE SERVICIO DIFERENTES
Frecuentemente, las vidas útiles de las alternativas de localización están relacionadas directamente con las de las máquinas o de los equipos y no encajan con el periodo de análisis requerido o no son iguales entre sí.
Cuando existen varias alternativas de localización mutuamente excluyentes con vidas útiles o de servicio diferentes, aplicaremos el VPN y el VAUE según se indica:
-
Valor Presente Neto (VPN) con el método del Mínimo Común Múltiplo (MCM). Si dos o más alternativas de localización mutuamente excluyentes tienen diferentes vidas útiles o de servicio, se deben evaluar utilizando un periodo igual al MCM de sus vidas útiles. En este caso, las vidas útiles de cada una de las alternativas se repetirán exactamente igual de manera sucesiva hasta alcanzar el número de periodos dado por el MCM. Cuando se utiliza este método, todas las alternativas que se consideran en la evaluación concluyen al mismo tiempo.
-
Valor Anual Uniforme Equivalente (VAUE) estableciendo un periodo de planeación o periodo de estudio, el cual se determina de forma un tanto arbitraria, independientemente de la vida útil de las alternativas de localización. Por ejemplo, si un proyecto tiene dos alternativas de localización, una con 6 años y otra con 8 años de vida útil, el horizonte de planeación puede ser 6 años, 8 años, o bien, cualquier otro, por ejemplo 4 años. Una vez que se establece el horizonte de planeación, las vidas útiles de las alternativas se igualan al horizonte de planeación, obligando a ajustar el valor de salvamento.
Vamos a tomar el ejemplo desarrollado en el proceso de selección de alternativas mutuamente excluyentes con vida útiles iguales, pero cambiando la vida útil de la alternativa “B” de 6 a 12 años.

SELECCIÓN DE ALTERNATIVAS DE LOCALIZACIÓN MUTUAMENTE EXCLUYENTES CON VIDAS ÚTILES DIFERENTES POR EL MÉTODO DEL VALOR PRESENTE NETO (VPN)
MCM (6,12) = 12
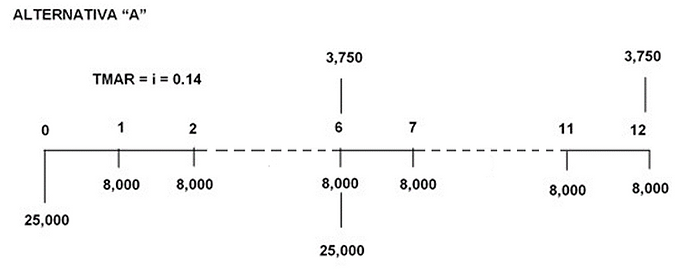

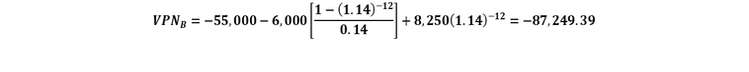
SELECCIÓN DE ALTERNATIVAS DE LOCALIZACIÓN MUTUAMENTE EXCLUYENTES CON VIDAS ÚTILES DIFERENTES POR EL MÉTODO DEL VALOR ANUAL UNIFORME EQUIVALENTE (VAUE)
Si utilizamos el criterio del VAUE y se establece un horizonte de evaluación igual a la vida útil menor de la alternativa A, estaríamos eliminando seis años de la vida útil de la otra alternativa y para hacer una comparación válida es necesario calcular el valor de salvamento de la alternativa B al término de seis años. Existen diversas formas para calcular el valor de salvamento antes del fin de su vida útil. Una manera sencilla de hacerlo es suponer que la pérdida de valor es lineal. Si se utiliza este supuesto, que es bastante empleado en la práctica, se aplica la siguiente fórmula:
Donde:
St = Valor de Salvamento al cabo de t años
I = Costo inicial (inversión)
S = Valor de Salvamento al término de la vida útil
n = Vida útil o de servicio


Según el VAUE, también se debe elegir la alternativa A por ser la de menor costo.
MODELOS DE OPTIMIZACIÓN
PLANTAS Y ALMACENES
Consideraremos una red entera desde el proveedor al consumidor, es decir, una cadena de suministro en la cual los proveedores envían materiales a las fábricas que proveen a los almacenes que a su vez abastecen los mercados como se ilustra en la siguiente figura.
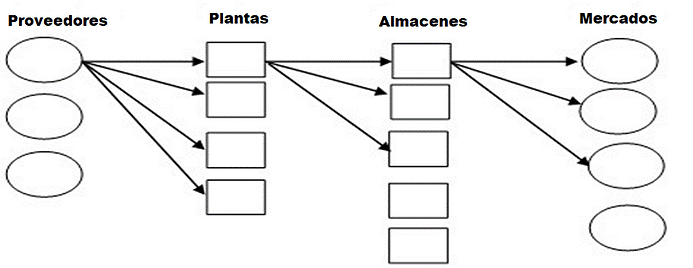
Las decisiones sobre la localización y la asignación de la capacidad tienen que tomarse tanto para las fábricas como para los almacenes. Se pueden emplear muchos almacenes para satisfacer la demanda de un mercado y también se pueden utilizar muchas fábricas para abastecer a los almacenes. También se supone que todas las unidades se han ajustado de manera apropiada para que una unidad de insumo de una fuente de suministro produzca una unidad de producto terminado.
El modelo requiere los siguientes datos:
m = número de mercados o puntos de demanda
n = número de posibles localizaciones de fábricas
l = número de proveedores
t = número de posibles localizaciones de almacenes
Dj = demanda anual del cliente j
Ki = capacidad potencial de la fábrica en el sitio i
Sh = capacidad de suministro del proveedor h
We = capacidad potencial del almacén en el sitio e
Fi = costo fijo de localizar la planta en el sitio i
fe = costo fijo de localizar el almacén en el sitio e
chi = costo de enviar una unidad de la fuente de suministro h a la fábrica i
cie = costo de producir y enviar una unidad de la fábrica i al almacén e
cej = costo de enviar una unidad del almacén e al cliente j
Definimos las siguientes variables de decisión:
yi =1 si la fábrica se localiza en el sitio i; 0 en caso contrario
ye = 1 si el almacén se localiza en el sitio e; 0 en caso contrario
xej = cantidad enviada del almacén e al mercado j
xie = cantidad enviada de la fábrica en el sitio i al almacén e
xhi = cantidad enviada del proveedor h a la fábrica en el sitio i
El problema se formula como el siguiente programa entero:
Función objetivo:
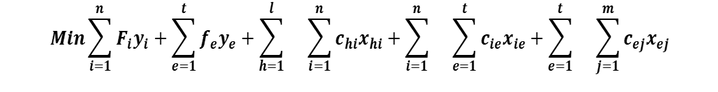
La función objetivo minimiza los costos totales fijos y variables de la red de la cadena de suministro sujeto a las siguientes restricciones:
Restricción respecto a la capacidad del proveedor:
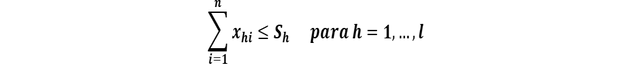
La cantidad total enviada desde un proveedor no puede exceder su capacidad.
Restricción de balance en la fábrica: cantidad enviada (producida) ≥ materia prima recibida

La cantidad enviada fuera de la fábrica no puede exceder la cantidad de la materia prima recibida.
Restricción respecto a la capacidad de la fábrica:
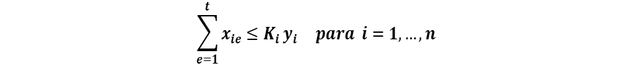
La cantidad producida en la fábrica no debe rebasar su capacidad.
Restricción de balance en el almacén: cantidad enviada ≤ cantidad recibida

La cantidad enviada fuera del almacén no puede rebasar la cantidad recibida de las fábricas.
Restricción respecto a la capacidad del almacén:

La cantidad enviada a través de un almacén no puede rebasar su capacidad.
Restricción respecto a la satisfacción de la demanda:

La cantidad enviada a un cliente debe cubrir la demanda.
Restricción de no negatividad:
Todas las cantidades enviadas a través de la red deber ser cero o positivas.
Restricción de variable binaria:
CASO 8:
En un proyecto de inversión del sector industrial se desea elegir la mejor alternativa de tamaño y localización. Se tiene que satisfacer la demanda de tres lugares:

Se considera que los costos significativos de transporte, en soles por unidad, son los siguientes:

La inversión necesaria de acuerdo al tamaño de planta y los costos de producción son los siguientes:

Los costos fijos representan el 45% de la inversión realizada en la construcción de la planta.
Se considera que los precios de venta son constantes e iguales en los tres lugares de consumo y que el tamaño de planta por lugar no puede exceder de 8,000 unidades.
Se pide elegir la mejor alternativa para decidir la localización y tamaño de planta donde los costos anuales de producción y de transporte sean mínimos.
La formulación del modelo es el siguiente:
Xij = cantidad enviada desde la planta i hasta el sitio j; i = j = 1, 2, 3
X11 = cantidad enviada desde A hasta A
X12 = cantidad enviada desde A hasta B
.
.
X33 = cantidad enviada desde C hasta C
Yit = 1 si en el sitio i se localiza una planta de tamaño t; 0 en caso contrario; (i = 1, 2, 3, 4, 5)
Y11 = planta localizada en A de tamaño 2000 unidades
Y12 = planta localizada en A de tamaño 4000 unidades
.
.
Y34 = planta localizada en C de tamaño 8000 unidades
Pit = cantidad producidas en planta localizada en i de tamaño t
P11 = cantidad producida en planta localizada en A de tamaño 2000 unidades
P12 = cantidad producida en planta localizada en A de tamaño 4000 unidades
.
.
P34 = cantidad producida en planta localizada en C de tamaño 8000 unidades
Función objetivo:
Minimizar el Costo Total = Costo Transporte + Costo Variable Producción + Costo Fijo
Min 5X11 + 20X12 + 40X13 + 20X21 + 6X22 + 30X23 + 40X31 + 30X32 + 8X33 + 8P11 + 6P12 + 4P13 + 2P14 + 8P21 + 6P22 + 4P23 + 2P24 + 8P31 + 6P32 + 4P33 + 2P34 + 450,000Y11 + 2,250,000Y12 + 4,500,000Y13 + 6,750,000Y14 + 450,000Y21 +...+ 6,750,000Y24 + 450,000Y31 + ... + 6,750,000Y34
Restricciones:
Restricciones de demanda:
X11 + X21 + X31 ≥ 3,000; demanda en A
X12 + X22 + X32 ≥ 5,000; demanda en B
X13 + X23 + X33 ≥ 6,000; demanda en C
Restricciones de balance envíos - producción:
X11 + X12 + X13 - P11 - P12 - P13 - P14 ≤ 0; producción en A
X21 + X22 + X23 - P21 - P22 - P23 - P24 ≤ 0; producción en B
X31 + X32 + X33 - P31 - P32 - P33 - P34 ≤ 0; producción en C
Restricciones de capacidad:
P11 - 2,000y11 ≤ 0; capacidad planta de 2,000 unidades en A
P12 - 4,000y12 ≤ 0; capacidad planta de 4,000 unidades en A
P13 - 6,000y13 ≤ 0; capacidad planta de 6,000 unidades en A
P14 - 8,000y14 ≤ 0; capacidad planta de 8,000 unidades en A
P21 - 2,000y21 ≤ 0; capacidad planta de 2,000 unidades en B
P22 - 4,000y22 ≤ 0; capacidad planta de 4,000 unidades en B
P23 - 6,000y23 ≤ 0; capacidad planta de 6,000 unidades en B
P24 - 8,000y24 ≤ 0; capacidad planta de 8,000 unidades en B
P31 - 2,000y31 ≤ 0; capacidad planta de 2,000 unidades en C
P32 - 4,000y32 ≤ 0; capacidad planta de 4,000 unidades en C
P33 - 6,000y33 ≤ 0; capacidad planta de 6,000 unidades en C
P34 - 8,000y34 ≤ 0; capacidad planta de 8,000 unidades en C
Restricciones tamaño planta:
P11 + P12 + P13 +P14 ≤ 8,000; producción en A
P21 + P22 + P23 + P24 ≤ 8,000; producción en B
P31 + P32 + P33 + P34 ≤ 8,000; producción en C
Restricciones de no negatividad:
Xij ≥ 0; i=1,2,3;j = 1, 2, 3
Pit ≥ 0; i = 1, 2 , 3; t = 1, 2, 3, 4
Restricciones de números binarios:
Yit ϵ {0,1}; para i = 1, 2, 3 ;t = 1, 2, 3, 4
SOLUCIÓN ÓPTIMA CON SOLVER DE EXCEL
Costo total de Producción (fijo+variable): S/5,946,000
Costo Total de Transporte : S/108,000
Costo Total : S/6,054,000
Ubicación de Plantas
Instalar en A una planta de 2,000 unidades.
Instalar en B una planta de 2,000 unidades.
Instalar en B una planta de 4,000 unidades.
Instalar en C una planta de 2,000 unidades.
Instalar en C una planta de 4,000 unidades.
Producción
Producir en la planta ubicada en A la cantidad de 2,000 unidades.
Producir en la planta ubicada en B la cantidad de 2,000 unidades.
Producir en la planta ubicada en B la cantidad de 4,000 unidades.
Producir en la planta ubicada en C la cantidad de 2,000 unidades.
Producir en la planta ubicada en C la cantidad de 4,000 unidades.
Envíos
Desde A hasta A, enviar la cantidad de 2,000 unidades.
Desde B hasta A, enviar la cantidad de 1,000 unidades.
Desde B hasta B, enviar la cantidad de 5,000 unidades.
Desde C hasta C, enviar la cantidad de 6,000 unidades.
SISTEMA DE DISTRIBUCIÓN
CASO 9
Una empresa opera una planta en el Callao con una capacidad anual de 40,000 unidades. El producto se embarca a centros regionales de distribución localizados en las regiones: Lima, La Libertad y Arequipa. Debido a que se espera un incremento en la demanda, la empresa planea aumentar su capacidad construyendo una planta nueva en una o más de las ciudades siguientes: Comas, Ate, Trujillo o Camaná. El costo fijo anual estimado y la capacidad anual para las plantas propuestas son los siguientes:
Planta Callao: 40,000 unidades
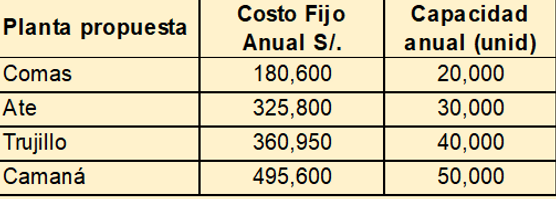
La empresa ha desarrollado los siguientes pronósticos de la demanda anual esperada en cada uno de los centros de distribución:

El costo de envío, en soles por unidad, desde cada planta a cada centro de distribución se muestra en la siguiente tabla:
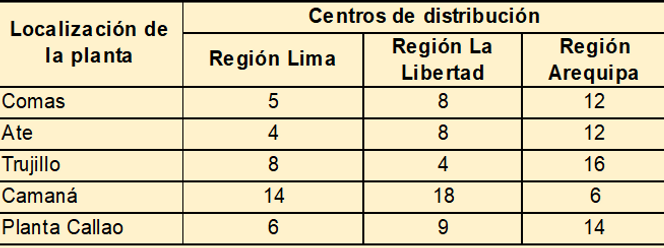
La siguiente figura es una representación de red del sistema de distribución, en la cual se indica cada ubicación potencial de la planta y las capacidades y demandas. Esta representación de red es para un problema de transporte (la capacidad total debe ser mayor o igual a la demanda total) con una planta en el Callao y los cuatro sitios propuestos para decidir cuál planta o plantas deben construirse.

SOLUCIÓN ÓPTIMA CON EXCEL
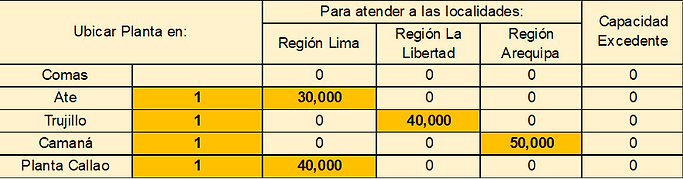
-
No instalar una planta en Comas para no incurrir en el costo fijo de S/180,600.
-
Se debe instalar en Ate una planta con capacidad igual a 30,000 unidades para atender la demanda de la Región Lima (30,000 unidades).
-
Se debe instalar en Trujillo una planta con capacidad igual a 40,000 unidades para atender la demanda de la Región La Libertad (40,000 unidades).
-
Se debe instalar en Camaná una planta con capacidad igual a 50,000 unidades para atender la demanda de la Región Arequipa (50,000 unidades).
-
La producción de la planta instalada en el Callao, con una capacidad de 40,000 unidades, servirá para atender la demanda de la Región Lima (40,000 unidades).
-
El costo total del sistema de distribución es igual a S/2,002,350.
MODELO DE TRANSPORTE
El objetivo del modelo de transporte es determinar el mejor patrón de embarque desde varios puntos de suministro (orígenes) hasta varios puntos de demanda (destinos) a fin de minimizar los costos totales de producción y transporte. Toda empresa con una red de puntos de suministro y demanda enfrenta este problema que puede modelarse de modo formal mediante programación lineal:
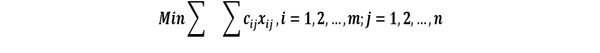
Sujeto a las siguientes restricciones:
Restricciones de suministro:
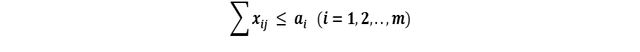
Restricciones de demanda:
Restricciones de no negatividad:
Donde:
CASO 10
Un proyecto está considerando fabricar cocinas a gas en tres plantas 1, 2 y 3 para enviarlas a cinco tiendas 1, 2, 3, 4 y 5 para su venta.
En la tabla N°1 se presenta la información de la demanda mensual requerida por cada una de las cinco tiendas; en la tabla N°2, la oferta mensual disponible de cada una de las tres plantas, y en la tabla N°3, los costos unitarios de suministro de cada planta a cada tienda.



Según un estudio adicional se determina que por razones físicas el origen 3 no puede surtir al destino 5.
Determinar un plan de distribución de costo mínimo que satisfaga todas las demandas en las tiendas mientras se asegura que los envíos desde las plantas de manufactura no excedan los suministros disponibles.
SOLUCIÓN
Paso 1: Balancear el problema, es decir lograr que Oferta = Demanda, es decir ∑ai = ∑bj
Si la oferta total es mayor que la demanda total, no se requiere realizar ninguna modificación en la formulación del problema. Sin embargo, si la oferta total es menor que la demanda total, se debe añadir un origen ficticio con una oferta igual a la diferencia entre la demanda total y la oferta total y asignando costos unitarios iguales a cero a todos los envíos de este origen ficticio para asegurar que no se realizarán envíos reales desde este origen.
En este caso, la oferta total es menor que la demanda total, por tanto añadimos el origen ficticio 4 con una oferta igual a la diferencia entre la demanda total y la oferta total (es decir, 50 unidades), y asignamos costos unitarios iguales a cero a todos los envíos de este origen.

Para asegurar que el origen 3 no surta al destino 5, al envío le asignamos un costo muy alto.
Paso 2: Con la matriz del problema balanceado, diseñamos una hoja de cálculo que nos permita aplicar Solver de Excel para obtener la solución óptima.
SOLUCIÓN ÓPTIMA CON SOLVER DE EXCEL

MODELO DE TRANSBORDO
CASO 11
Un proyecto considera producir un determinado electrodoméstico para el hogar con instalaciones de producción en Callao y Ate. Los electrodomésticos producidos en cualquiera de las instalaciones pueden enviarse a los almacenes localizados en Breña y Villa El Salvador. Desde estos centros de distribución, se abastecerá a las tiendas minoristas que se piensa ubicar en Lima, Los Olivos, Santa Anita y Chorrillos. La información clave del problema se muestra a continuación:

Se ha desarrollado los siguientes pronósticos de la demanda anual esperada en cada una de las tiendas minoristas (nodos de destino):

El costo de envío, en soles por unidad, desde cada planta (nodos de origen) a cada almacén (nodos de transbordo) se muestra en la siguiente tabla:
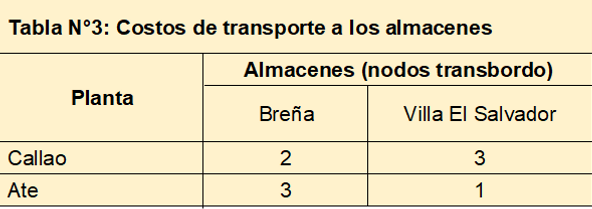
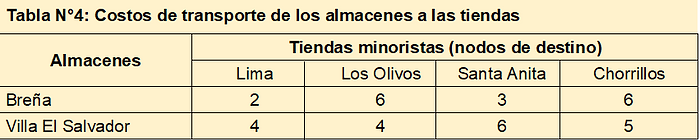
El problema está balanceado, es decir la oferta de los orígenes es igual a la demanda de los destinos, en este caso igual a 1000 unidades.
La siguiente figura es una representación de red del sistema de distribución, en la cual los nodos 1 y 2 son los nodos de origen; los nodos 3 y 4 son los de transbordo, y los nodos 5, 6, 7 y 8 son los de destino.

SOLUCIÓN ÓPTIMA CON SOLVER DE EXCEL

MODELO DE REDES
Muchos sitios como las instalaciones de emergencia, deben ubicarse cerca de las vías públicas por su facilidad de acceso. Así, la mejor localización debe tomar en cuenta los tiempos de recorrido.
Para resolver este tipo de problemas usaremos la programación entera binaria. Aquí nos centraremos en la selección de sitios para instalaciones de servicios de emergencia tales como: estaciones de bomberos, estaciones de policía, estaciones de serenazgo, centros de ambulancias y otras. En cualquiera de estos casos, la mayor preocupación es proporcionar instalaciones que estén lo suficientemente cercanas a cada una de las zonas del área a la que atienden para que el tiempo de respuesta a una emergencia en cualquier lugar dentro del área sea lo más pequeño posible. La forma del modelo de programación entera binaria que se presenta será básicamente la misma sin importar el tipo específico de servicios de emergencia que se esté considerando.
CASO 12
San Juan de Lurigancho es el distrito más poblado de Lima y también el que registra más casos de inseguridad ciudadana. La ciudad se ha vuelto un lugar muy peligroso para los pobladores y los visitantes, por lo que la Municipalidad distrital ha encargado la realización de un estudio para determinar en qué zonas se instala una estación de serenazgo de tal manera que se pueda atender cualquier emergencia en el tiempo máximo de 10 minutos para evitar daños a la población con una respuesta rápida por parte del personal de serenazgo.
Se decidió encontrar una solución al problema mediante la programación entera binaria. El distrito está dividido en ocho zonas, y se recopiló información respecto al tiempo esperado de respuesta para una emergencia desde una estación potencial de serenazgo en cada una de las ocho zonas. Estos datos aparecen en la tabla Nº1. Por ejemplo, si se tomara la decisión de ubicar una estación de serenazgo en la zona 1 y esa estación se utilizara para responder a una emergencia en cualquiera de las zonas, en la segunda columna de dicha tabla se muestra cuál sería el tiempo de respuesta (estimado). Como el tiempo de respuesta sería superior a 10 minutos para una emergencia en las zonas 4, 5, 6, 7 u 8, se necesitaría ubicar una estación de serenazgo más cerca de estas zonas para cumplir la nueva política del consejo de la ciudad. En el renglón inferior, de la referida tabla se muestra cuál sería el costo de construir una estación de serenazgo en cualquiera de las ocho zonas que cuentan con terrenos disponibles propiedad de la Municipalidad distrital. (Los costos menores para algunas de las zonas es porque cuentan con estaciones de serenazgo, por lo que sólo se necesita una renovación y mejorar el equipamiento).



El objetivo consiste ahora en determinar mediante la programación entera binaria, qué zonas deben recibir una estación de serenazgo para minimizar el costo total de las estaciones al mismo tiempo que se garantice que cada zona de la ciudad cuente con una estación suficientemente cercana para responder a una emergencia en no más de 10 minutos.
SOLUCIÓN
Para cada una de las seis zonas hay una decisión SÍ o NO respecto a qué zona debe recibir una estación de serenazgo. Por tanto, la variable de decisión es la siguiente:

Función Objetivo
ara cada una de las seis zonas hay una decisión SÍ o NO respecto a qué zona debe recibir una estación de serenazgo. Por tanto, la variable de decisión es la siguiente:

Restricciones
La municipalidad debe tener la certeza de que hay una estación de serenazgo a 10 minutos de cada zona.

Para asegurar que por lo menos una estación de serenazgo está a 10 minutos de la ciudad 1, se suma la restricción X1 + X2 + X3 = 1 para asegurar que sea imposible X1 = X2 = X3 = 1, de modo que por lo menos una estación se construirá a 10 minutos de la zona 1.
De esta manera, se determina el resto de restricciones.
Estas restricciones junto con el requerimiento de que las variables sean binarias son todo lo que se necesita para garantizar que cada zona cuente al menos con una estación de serenazgo cercana para responder a una emergencia en no más de 10 minutos.
SOLUCIÓN CON SOLVER DE EXCEL:
Se requiere construir 3 estaciones de serenazgo, en las siguientes zonas con un costo total igual a S/105,000:

Es difícil planear globalmente la localización de todos los elementos de la cadena de suministro, por esta razón es recomendable realizar estudios parciales para decidir, por ejemplo, la localización de las plantas respecto de la localización de los proveedores y los almacenes, o la localización de los centros de distribución en relación con la localización de las plantas y de las tiendas de atención al cliente.
Un centro de distribución permite obtener economías de escala con base en la consolidación de pedidos. Si no se utilizan centros de distribución, los pedidos se envían directamente desde diferentes plantas a los centros de demanda en cantidades pequeñas, mientras que los centros de distribución permiten recibir productos desde diferentes plantas, que luego serán consolidadas para su transporte en grandes volúmenes hacia los centros de demanda (tiendas).
¡Estamos ansiosos de escuchar sobre tus problemas relacionados con la localización de tu planta, almacén, centro de distribución o tienda!
Llámanos hoy mismo y ayúdanos a saber qué estás buscando.
NOTA IMPORTANTE
En el enlace de abajo puedes descargar gratis la hoja de cálculo con las soluciones de cada uno de los casos. Para la aclaración de cualquier duda o contar con nuestro apoyo para el planteamiento y resolución de casos más complejos, no dudes en ponerte en contacto con nosotros.






