PRODUCCIÓN
El proceso de producción es un conjunto de actividades mediante las cuales los factores productivos se transforman en productos con valor para los clientes. La transformación añade valor a los insumos adquiridos por la empresa, los cuales se convierten en más valiosos y aumentan su potencialidad para satisfacer las necesidades de los clientes a medida que avanzan a través del proceso de transformación.
PRINCIPALES PROBLEMAS DE PRODUCCIÓN
1 DECISIÓN DE FABRICAR O COMPRAR
Un comerciante, mayorista o minorista, compra todo lo que vende; sin embargo, un fabricante tiene que elegir entre los bienes y servicios que pueden obtenerse de un proveedor externo con ventaja, en lugar de producirlos internamente. Aquí presentamos el uso del análisis del punto de equilibrio para ayudar al emprendedor a tomar las mejores decisiones respecto a fabricar o comprar.
El emprendedor frecuentemente tiene que tomar la decisión de FABRICAR o COMPRAR, es decir, puede comprar el producto de un proveedor externo a C1 por unidad, pero puede producirlo por un costo por unidad menor, C2 < C1; sin embargo, para poder producir el producto, el emprendedor debe invertir F unidades monetarias (costo fijo) para construir la planta o taller con la capacidad de producción suficiente para atender la demanda de un determinado mercado.
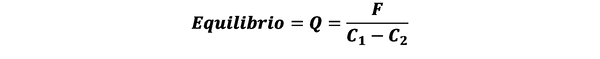
CASO N°1.1: OPCIÓN DE COMPRAR SIN COSTO FIJO
Se trata de un proyecto para producir un nuevo modelo de una máquina industrial y el emprendedor debe decidir si lo produce o si lo compra a un proveedor de la China. El proveedor está dispuesto a fabricar y vender el producto en S/1,200 por unidad, pero el emprendedor estima que puede producirlos por S/800 la unidad. Asimismo, estima que para instalar la planta y comprar el equipo necesario costaría S/600,000. Considerando la demanda anual estimada de 2,000 máquinas, el emprendedor ¿debe producir o comprar la máquina?
Solución:
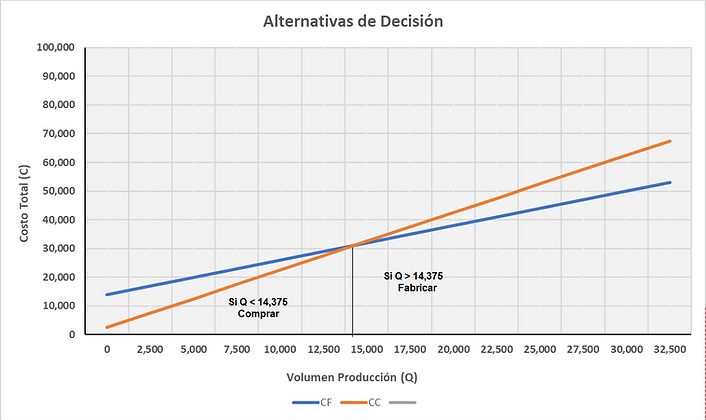
Para una producción de 1,500 unidades, es indiferente fabricar o comprar porque ambas alternativas tienen el mismo costo igual a A/1,800,000; sin embargo, para atender la demanda se requiere producir 2,000 unidades y para este nivel de producción conviene producir porque esta alternativa tiene un costo menor que la de comprar:
Gráfica del Punto de Equilibrio
Plan de Decisión



CASO N°1.2: OPCIÓN DE COMPRAR CON COSTO FIJO
En un proyecto de inversión sobre un restaurante de comida rápida que incluirá ensaladas en el menú, existen dos opciones sobre las ensaladas:
1. La opción de fabricar consiste en instalar una barra de ensaladas bien provista de hortalizas, frutas y aderezos, y dejar que el cliente prepare su propia ensalada. La barra de ensaladas tendría que pedirse en alquiler y sería necesario contratar un empleado de tiempo parcial que la atendiera. Se estima los costos fijos en S/14,000 y el costo variable unitario en S/1.2 por ensalada.
2. La opción de comprar consiste en conseguir las ensaladas ya preparadas y listas para la venta. Éstas tendrían que comprarse a un proveedor local a S/2 por ensalada. La venta de ensaladas previamente preparadas requerirá la instalación y operación de más frigoríficos con un costo fijo anual de S/2,500.
Considerando que se espera vender 28,000 menús al año y que el precio para el cliente será el mismo con cualquiera de las opciones, ¿qué opción es mejor: fabricar o comprar?
Solución:
Gráfica del Punto de Equilibrio
Plan de Decisión

CASO N°1.3: FABRICAR O COMPRAR - MODELO DE PROGRAMACIÓN LINEAL
En un proyecto de emprendimiento para fabricar y comercializar dos traductores de idiomas electrónicos, el problema es determinar cuánto, de cada uno de los diversos componentes, debe producir el proyecto, y cuánto deberá adquirir de un proveedor externo. Se pretende introducir dos nuevos dispositivos electrónicos traductores de idiomas en tiempo real:
Modelo A: Admite la traducción de hasta 16 idiomas, como inglés, español, chino, japonés, etc. Se habla con el auricular, y luego se traduce a la voz del país que se desea. Permite una transmisión de audio estable y rápida, también tiene conexión inalámbrica de hasta 10 metros, fácil de conectar a diversos dispositivos en segundos.
Modelo B: Hace traducción de 33 idiomas diferentes como: inglés, chino, coreano, japonés, tailandés, francés, alemán, español, italiano, holandés, griego, portugués, ruso, árabe, sueco, checo, finlandés, danés, polaco, húngaro, rumano, y más. Es una buena opción para los que viajan al extranjero, chatear con amigos extranjeros y traducir cuando se va de compras o para cuando se viaja por trabajo.
Para fines de simplificar la solución vamos a suponer que cada dispositivo electrónico tiene tres componentes: una carcasa, un componente 1 y un componente 2. En ambos dispositivos se utiliza la misma carcasa, pero los otros componentes son diferentes. El proyecto puede fabricar todos los componentes, o puede adquirirlos de proveedores externos. Los costos de fabricación y los precios de adquisición de los componentes se resumen en la siguiente tabla:
Los pronósticos de demanda son los siguientes: 3,00 unidades modelo A y 2,000 unidades modelo B.
Por restricciones de capital la capacidad de producción de los dispositivos es la siguiente: 200 horas mensuales de tiempo normal de fabricación (8 horas diarias por 25 días laborables al mes) y 50 horas mensuales de tiempo extra (25% del tiempo normal, se considera 2 horas extras diarias por trabajador). A cada trabajador se le pagará la RMV vigente de S/930. A continuación, se muestra los tiempos de fabricación (en minutos) de dichos componentes:
El problema al que se enfrenta el emprendedor es determinar cuántas unidades de cada componente debe fabricar y cuántas adquirir de un proveedor externo.
Solución:
De acuerdo a la información disponible se determina que una hora de tiempo normal cuesta S/3.875 y una hora extra 25% más, es decir, S/4.84375 por las dos primeras horas extras.
Este problema lo resolveremos mediante un modelo de programación lineal.
Variables de decisión:
CF = Número de carcasas fabricadas
CA = Número de carcasas adquiridas
C1AF = Número de componentes 1 Modelo A fabricados
C1AA = Número de componentes 1 Modelo A adquiridos
C1BF = Número de componentes 1 Modelo B fabricados
C1BA = Número de componentes 1 Modelo B adquiridos
C2AF = Número de componentes 2 Modelo A fabricados
C2AA = Número de componentes 2 Modelo A adquiridos
C2BF = Número de componentes 2 Modelo B fabricados
C2BA = Número de componentes 2 Modelo B adquiridos
HE = Número de horas de tiempo extra a programar
Función Objetivo:
La función objetivo es minimizar el costo total, incluyendo costos de manufactura, de adquisición y de tiempo extra. Utilizando los datos de costos unitarios y la tasa de costo por tiempo extra, escribimos la función objetivo de la siguiente forma:
Minimizar Costos = Manufactura + Adquisición + Tiempo Extra
Mín 5CF + 6CA + 37.5C1AF + 40C1AA + 33C1BF + 39C1BA + 6C2AF + 6.5C2AA + 7.5C2BF + 7.8C2BA + 4.84375HE
Restricciones de Demanda
Las restricciones de demanda definen la cantidad que se debe obtener de cada componente para satisfacer la demanda de 3,000 unidades Modelo A y 2,000 unidades Modelo B.
Se necesita un total de 5,000 carcasas, y el volumen de producción de los otros dos componentes depende de la demanda de cada modelo en particular. Las restricciones de demanda son:
CF + CA = 5,000 Carcasas (Modelo A + Modelo B)
C1AF + C1AA = 3,000 Componentes 1 Modelo A
C1BF + C1BA = 2,000 Componentes 1 Modelo B
C2AF + C2AA = 3,000 Componentes 2 Modelo A
C2BF + C2BA = 2,000 Componentes 2 Modelo B
Restricciones de Capacidad
Se necesitan dos restricciones para garantizar que no se exceda la capacidad de producción en tiempo tanto normal como extra. La primera restricción limita la capacidad del tiempo extra a 50 horas, esto es:
HE ≤ 50
La segunda restricción expresa que el tiempo total de manufactura necesario para todos los componentes debe ser menor que o igual a la capacidad de producción, incluyendo tiempo normal y extra.
El tiempo de fabricación de los componentes se expresa en minutos, por lo que expresamos la restricción de capacidad total de producción en minutos, convirtiéndose las 200 horas de capacidad en tiempo normal en 60x200 = 12,000 minutos. En este momento el tiempo extra necesario es desconocido, por lo que escribiremos el tiempo extra como 60HE. Utilizando los tiempos de fabricación, tenemos:
CF + 3C1AF + 2.5C1BF + C2AF + 1.5C2BF ≤ 12,000 + 60HE
Pasando la variable de decisión correspondiente al tiempo extra al lado izquierdo de la restricción, obtenemos la restricción por capacidad de producción:
CF + 3C1AF + 2.5C1BF + C2AF + 1.5C2BF - 60HE ≤ 12,000
Restricciones de No Negatividad
Variables de decisión ≥ 0
Solución con SOLVER de Excel
También es posible realizar un análisis de sensibilidad con SOLVER de Excel.



En los enlaces de abajo puedes descargar gratis las hojas de cálculo con las soluciones de cada uno de los casos. Para la aclaración de cualquier duda o contar con nuestro apoyo para el planteamiento y resolución de casos más complejos, no dudes en ponerte en contacto con nosotros.
2 PLANEACIÓN AGREGADA DE LA PRODUCCIÓN
Es la planeación macro de la producción que puede utilizar el emprendedor para tomar decisiones sobre cuántos trabajadores debe contratar y qué cantidad y mezcla de productos debe producir. Este tipo de planeación comienza con el pronóstico de la demanda de bienes y/o servicios y la velocidad de respuesta frente a los cambios de la demanda depende de varios factores, entre ellos, de la estrategia que se adopte en cuanto a conservar o despedir a los trabajadores y mantener inventarios.
PLAN DE CERO INVENTARIOS
El Plan Cero Inventarios consiste en producir cada periodo justo la cantidad demandada, sin inventarios. Este plan es una estrategia de planeación agregada de la producción que consiste en modificar el tamaño de la fuerza laboral con la finalidad de satisfacer o perseguir la demanda. No requiere mantener inventarios (cero inventarios), la fuerza de trabajo absorbe los cambios en la demanda a través de un flujo de contrataciones y despidos de trabajadores temporales.
Contratar y/o despedir temporalmente a trabajadores para ajustar las tasas de producción requiere de una capacitación frecuente y la productividad baja temporalmente hasta que se integren en el proceso productivo. Los despidos o la finalización de contratos, traen también como consecuencia una caída en la moral de los trabajadores y pueden desembocar en una menor productividad. Este plan utiliza la capacidad como palanca y debe usarse cuando el costo de manejo del inventario es alto y los costos de cambiar los niveles de producción de máquinas y capacidad de mano de obra son bajos.
CASO N°2.1: PLAN CERO INVENTARIOS
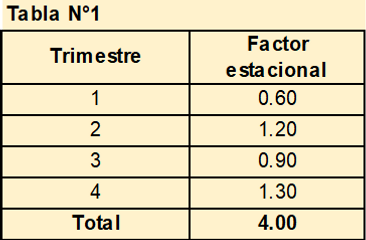
El pronóstico de la demanda es de 15,000 unidades anuales. Los factores estacionales trimestrales son los siguientes:
Los factores estacionales se asignan según la naturaleza del negocio. Por ejemplo, si se trata de un producto cuya demanda generalmente baja en el primer trimestre de cada año porque se ve afectado por los gastos escolares, entonces el factor debe ser menor que 1, caso contrario debe ser mayor que 1. La suma de los cuatro factores estacionales debe ser igual a 4. En este caso, por ejemplo, estamos asumiendo que es muy probable que la demanda baje 40% durante el primer trimestre.
Número de horas de trabajo en tiempo regular: 8 horas/día.
Para el cálculo del Costo de la Mano de Obra Directa se cuenta con la siguiente información:
Según estudios se ha determinado que una unidad de producto se produce en 1.5 horas/unidad. Considerando que la remuneración Mínima Vital (RMV) vigente es S/930, el costo de la mano de obra directa en tiempo regular es igual a 3.875S/hora-ordinaria. Ahora, tomando en cuenta el tiempo de producción unitario, el costo de la mano de obra directa por producto es igual a 5.8125S/unidad.
Los Costos Indirectos de Fabricación se han estimado en S/1.10 por unidad.
El costo de producción (MD+MOD+CIF) es igual a S/11.525 por unidad.
Los Gastos de Administración y Ventas (GAV) representan aprox. el 10%(MD+CIF+MOD), es decir, los GAV es igual a S/1.15125 por unidad.
El costo total (MD+MOD+CIF+GAV) es igual a S/12.66375 por unidad.
La utilidad esperada representa el 20% sobre el costo total, esto equivale a S/2.53275 por unidad.
El costo de faltantes es el costo de oportunidad de pedidos no atendidos que vamos a considerar igual al margen de utilidad unitario, esto es S/2.53275 por unidad faltante.
El Precio de Venta (Costo Total + Utilidad) es S/15.1965 por unidad.
Costo del tiempo extra (primeras dos horas) 25% más de S/3.875 = 4.84375 S/hora-extra.
Número de horas extras permitidas por trabajador 25%(8) = 2 horas de sobretiempo por día.
Costo de mantenimiento de inventario 25% del costo de producción, es decir 25%(11.5125) = 2.878125 S/unidad/trimestre.
El costo de mantenimiento de inventario incluye costo de capital, costos variables de almacenamiento, obsolescencia y deterioro. Generalmente se expresa como un porcentaje del valor monetario del inventario (entre 15% a 5% por año). Este costo puede considerarse como un cargo de intereses aplicado contra el valor monetario del inventario que se mantiene en el almacén; por ejemplo, si el costo de mantenimiento es de 20% y cada unidad tiene un costo de producción de S/10, costará S/2 mantener una unidad en el inventario durante un año.
Costo de contratación y capacitación: S/150/trabajador. Este costo se estima considerando el tiempo y los recursos invertidos en las fases de reclutamiento, selección, inducción y capacitación interna para conferir al nuevo trabajador la destreza requerida por el proceso productivo.
Costo de despido para un trabajador Microempresa S/371/trabajador-trimestre. El costo de despido comprende las indemnizaciones y otros costos legales asociados, según el régimen laboral. En este caso se trata de un despido por término de contrato laboral. Multiplicamos la RMV por 1.5, el resultado lo dividimos por 12 y luego lo multiplicamos 3 meses que es el periodo de contrato (trimestral). Finalmente, a este resultado le añadimos los beneficios laborales.
Costo de subcontratación 20 S/unidad. El costo de subcontratación es el precio que se paga a otra empresa para la producción de las unidades requeridas. Este costo se obtiene de las cotizaciones realizadas a diversos proveedores que tienen capacidad para producir el producto.
Como se trata de un proyecto de nueva empresa, se entiende que al inicio no existe inventario inicial de producto terminado (I0 = 0) ni trabajadores disponibles (W0 = 0). Asimismo, no hay una política de inventarios ni de órdenes atrasadas o faltantes, los cuales se definirán según los requerimientos en cada plan de producción.
I0 = 0 unidades a inicio del primer trimestre
W0 = 0 trabajadores al inicio de operaciones
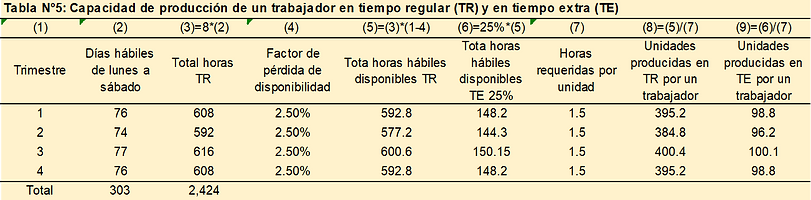
Producción de un trabajador por día: una unidad se produce en 1.5 horas, además se considera un factor de pérdida de disponibilidad de 2.5%, por tanto, en 8 horas la producción es 5.2 unidades/día.
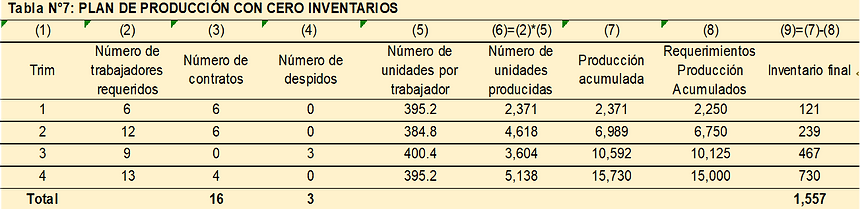
SOLUCIÓN PLAN DE PRODUCCIÓN CERO INVENTARIOS - MÉTODO HEURÍSTICO
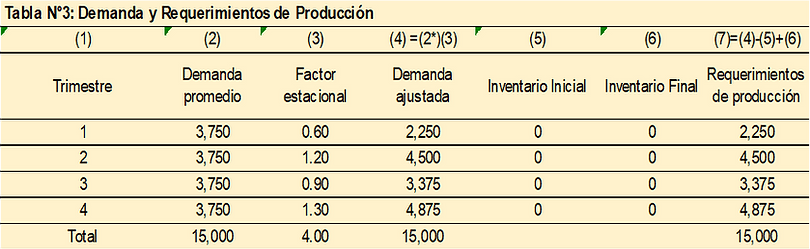
Teóricamente no existe inventario final, por tanto, los valores de esta columna deberían ser iguales a cero; sin embargo, por efecto del redondeo en el número mínimo de trabajadores, en el número de unidades producidas, etc. se generan inventarios, en este caso 1,557 unidades.
Costo del plan sin permitir tiempo ocioso o inactivo
(+) Costo Contrataciones : S/2,400
(+) Costo Despidos : S/1,113
(+) Costo Inventario : S/4,482
(+) Costo MOD : S/93,775
(+) Costo MD : S/72,358
(+) Costo CIF : S/17,303
(=) Costo Total : S/191,431
Costo del plan permitiendo tiempo ocioso o inactivo
(+) Costo Contrataciones : S/2,400
(+) Costo Despidos : S/1,113
(+) Costo Tiempo Ocioso : S/4,352
(+) Costo MOD : S/89,4235
(+) Costo MD : S/69,000
(+) Costo CIF : S/16,500
(=) Costo Total : S/182,788
En este caso, conviene el Plan Cero Inventarios Con Tiempo Ocioso porque tiene un costo total de S/182,788, el cual significa S/8,643 menos que el costo total del Plan Cero Inventarios Sin Tiempo Ocioso.
SOLUCIÓN PLAN DE PRODUCCIÓN CERO INVENTARIOS - MODELO DE PROGRAMACIÓN LINEAL
Variables del modelo
Wt = Cantidad de trabajadores temporales al inicio del periodo t, después de cualquier contratación o despido
Ht = Cantidad de trabajadores temporales contratados al inicio del periodo t
Lt = Cantidad de trabajadores temporales despedidos al inicio del periodo t
It = Unidades de inventario final para el periodo t
Costos
CHt = Costo de contratación de un trabajador al inicio del periodo t = S/150
CLt = Costo de despido de un trabajador al inicio del periodo t = S/371
CIt = Costo de inventario por unidad por periodo t = S/2.878125
MDt = Costo de material directo por unidad producida en el periodo t = S/4.6
CIFt = Costo indirecto de fabricación por unidad producida en el periodo t = S/1.1
Producción
Pt = Producción en unidades en el periodo t
P1 = Producción en unidades en el periodo 1 = 395.2 unidades/trabajador
P2 = Producción en unidades en el periodo 2 = 384.8 unidades/trabajador
P3 = Producción en unidades en el periodo 3 = 400.4 unidades/trabajador
P4 = Producción en unidades en el periodo 4 = 395.2 unidades/trabajador
Función objetivo
Minimizar Costo Total = Costo Mano de Obra + Costo Contrataciones + Costo Despidos + Costo Inventarios
Los costos incluidos en la función objetivo anterior son relevantes porque cambian según la decisión que se tome, sin embargo, también puede incluirse los costos de materiales directos y los costos indirectos de fabricación para determinar el costo total del plan.
CMDt = Costo de materiales directos por unidad producida en el periodo t
CIFt = Costo indirecto de fabricación por unidad producida en el periodo t
Restricciones
Fuerza de trabajo
Balance de Inventario
Balance de Capacidad
Restricciones de No Negatividad
SOLUCIÓN CON SOLVER DE EXCEL
El costo del plan con el método de programación lineal es S/181,572, el cual es menor que el obtenido con el método heurístico en S/9,859. Sin embargo, como la programación lineal arroja inventarios y productos fraccionarios, es necesario redondear a enteros obteniéndose los siguientes resultados:
Costo del plan sin permitir tiempo ocioso o inactivo
(+) Costo Contrataciones : S/2,550
(+) Costo Despidos : S/1,484
(+) Costo Inventario : S/2,178
(+) Costo MOD : S/91,388
(+) Costo MD : S/70,516
(+) Costo CIF : S/16,863
(=) Costo Total : S/184,978
El costo total con valores redondeados del plan con el método de programación lineal es S/184,978, el cual es menor que el obtenido con el método heurístico en S/6,453.





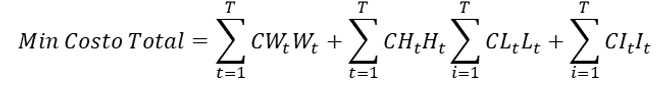

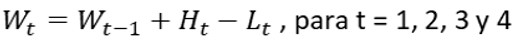


El plan de producción se puede elaborar con técnicas heurísticas o de programación lineal. Para la aclaración de cualquier duda o contar con nuestro apoyo para el planteamiento y solución de casos más complejos, no dudes en ponerte en contacto con nosotros.
La solución de diversos problemas de plan de producción en Excel lo puedes descargar desde el siguiente enlace.

3 PROGRAMACIÓN DE LA PRODUCCIÓN
El emprendedor debe determinar los niveles de producción que le permitan cumplir con la demanda, dadas las restricciones o limitaciones en capacidad de producción, capacidad de mano de obra, espacio de almacenamiento y, al mismo tiempo, minimizar el costo de producción.
CASO 3.1
El proyecto consiste en brindar el servicio de producción de dos componentes electrónicos para una gran empresa, la cual notificará cada trimestre sus necesidades mensuales de componentes de los tres meses siguientes, que pueden variar significativamente en función de la demanda de la gran empresa. Vamos a considerar que en diciembre del 2020 la gran empresa remite la siguiente orden de producción:
Una vez procesada la orden, se enviará una notificación de demanda al área de producción para que desarrolle un plan de producción a tres meses. Para llegar al programa deseado, se requiere determinar:
1. Costo de producción
2. Costo de inventarios
3. Costo de suavización de la producción
Se cuenta con la siguiente información adicional:
El costo de producción de una unidad de C-1 es S/20, y de una unidad de C-2 es S/10. El costo de mantener inventario es igual al 15% del costo de producción. El costo asociado con el incremento del nivel de producción para cualquier mes es S/0.50 por unidad, y el correspondiente a la reducción del nivel de producción es S/0.20 por unidad.
No existen inventarios iniciales y también no se desea tener inventarios al final del periodo de planeamiento.
SOLUCIÓN CASO 3.1: Programación lineal




4 ASIGNACIÓN DE LA FUERZA DE TRABAJO
Los emprendedores tienen que tomar decisiones que involucran requerimientos de personal para un periodo de planeación determinado. Las asignaciones de la fuerza de trabajo tienen cierta flexibilidad para que parte del personal pueda asignarse a más de un departamento o centro de trabajo, por esta razón se requiere capacitar a los trabajadores en forma cruzada en dos o más puestos.
En el caso que sigue mostramos cómo utilizar la programación lineal para determinar no solamente cuál es la mezcla óptima del producto, sino también cuál es la asignación óptima de la fuerza de trabajo.
CASO 4.1
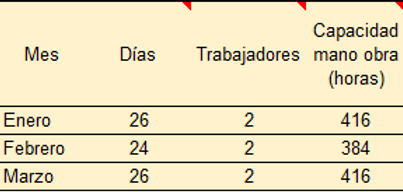
El proyecto es para fabricar dos productos con contribuciones a la utilidad. En la siguiente tabla se muestra las necesidades de mano de obra por unidad producida y las horas totales de mano de obra disponible por personal asignado a cada uno de los cuatro departamentos que tendrá la futura empresa.
Contribución a la utilidad de P-1: S/10
Contribución a la utilidad de P-2: S/9

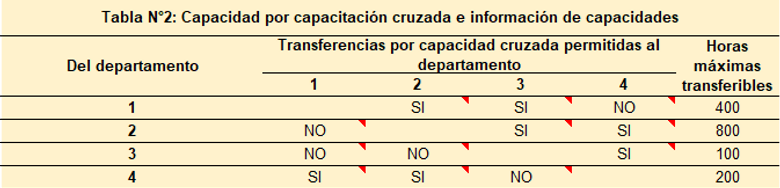
El proyecto tiene previsto una capacitación cruzada para permitir que algunos trabajadores puedan ser transferidos entre departamentos. Aprovechando estas habilidades de capacidad cruzada, un número limitado de trabajadores y de horas de mano de obra pueden transferirse de un departamento a otro. Por ejemplo, suponga que la capacitación cruzada permite transferencias según se puede observar en la tabla siguiente:
SOLUCIÓN 4.1: PROGRAMACIÓN LINEAL
Utilidad Total: S/84,011.
Mezcla óptima de productos:
Producto 1: 6,825 unidades
Producto 2: 1,751 unidades
Transferencia de fuerza de trabajo:
La mezcla óptima de productos de 6,825 unidades del producto 1 y 1,751 unidades del producto 2, se puede conseguir siempre que se transfieran 400 horas del departamento 1 al 3; 651 horas del departamento 2 al 3 y 149 horas del departamento 2 al 4.
Las asignaciones resultantes de la fuerza de trabajo para los departamentos 1 a 4 alcanzarán 6,100; 5,200; 8,051; y 1,549 horas respectivamente.
Si se tiene la flexibilidad de asignar personal a distintos departamentos, debería resultar en menor tiempo ocioso de la fuerza de trabajo, mejor utilización de la fuerza de trabajo y mayor utilidad.
Este modelo de programación lineal automáticamente asigna trabajadores y horas de mano de obra a los departamentos de la manera más redituable posible.
5 COMBINACIÓN DE RECURSOS
Siempre que un emprendedor deba decidir cómo combinar dos o más recursos para producir uno o más productos se dan problemas de mezclas. En estas situaciones, los recursos contienen uno o más ingredientes esenciales que deben mezclarse en productos terminados que contendrán porcentajes específicos de cada uno de ellos. En la mayoría de estas aplicaciones, se debe decidir cuánto adquirir de cada recurso para satisfacer las especificaciones del producto y las demandas del mismo a un costo mínimo.
CASO 5.1
El proyecto producirá refrescos de frutas, uno normal y otro light, que se venderán a precios diferentes en los mercados de Lima y Callao. Los refrescos de frutas se producirán mezclando tres componentes que tienen costos diferentes. Se requiere determinar cómo mezclar los tres componentes en la producción de los dos tipos de refrescos, de tal forma que se logre maximizar las utilidades.
Los precios de venta de los refrescos son los siguientes: Refresco Normal S/3 por litro y Refresco Light S/4 por litro. Para el periodo actual de planeación de la producción, se puede obtener los tres componentes al costo por litro y en las cantidades que se muestran en la Tabla N°1:
Las especificaciones del producto para los refrescos normal y light limitan las cantidades de cada componente que se pueden utilizar en cada refresco. La Tabla N°2 enlista las especificaciones de los productos. Las restricciones con los distribuidores requieren que el proyecto produzca por lo menos 10,000 litros de refresco normal.
El problema es determinar cuántos litros de cada componente se deberá utilizar en la mezcla del refresco normal y cuántos en la de refrescos light. La solución de mezcla óptima deberá maximizar la utilidad, sujeto a las restricciones de suministros disponibles, a las especificaciones de los productos, y a los 10,000 litros requeridos de refrescos normal.
SOLUCIÓN ÓPTIMA CASO 5.1: PROGRAMACIÓN LINEAL
La estrategia óptima de mezclado muestra que deben producirse 10,000 litros de refrescos normal.
El refresco normal debe producirse utilizando solamente los 10,000 litros del componente 2. Mientras que los 15,000 litros de refresco light debe producirse como una mezcla de 5,000 litros del componente 1 y 10,000 litros del componente 3.
La utilidad total que se obtiene con esta estrategia óptima de mezcla es S/.75,500, correspondiendo S/.24,000 al refresco normal y S/.49,500 al refresco ligth.









